
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1218 Атанасян — Подробные Ответы
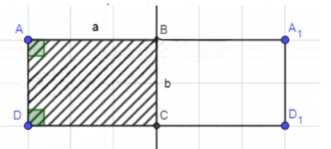
Один цилиндр получен вращением прямоугольника ABCD вокруг прямой AB, а другой цилиндр — вращением этого же
прямоугольника вокруг прямой ВС. а) Докажите, что площади боковых поверхностей этих цилиндров равны. б) Найдите отношение площадей полных поверхностей этих цилиндров, если AB = а, ВС = b.
Дано: \(ABCD\) — прямоугольник; \(AB = a\); \(BC = b\);
Доказать: а) \(S_{1 \text{бок}} = S_{2 \text{бок}}\); Найти: б) \(\frac{S_1}{S_2} = ?\);
Решение:
а) Рассмотрим осевые сечения тел вращения:
\(S_{1 \text{бок}} = 2\pi \cdot BC \cdot AB = 2\pi ba\);
\(S_{2 \text{бок}} = 2\pi \cdot AB \cdot BC = 2\pi ab\);
Следовательно, \(S_{1 \text{бок}} = S_{2 \text{бок}}\), что и требовалось доказать.
б) \(S_1 = 2\pi \cdot BC(BC + AB) = 2\pi b(b + a)\);
\(S_2 = 2\pi \cdot AB(AB + BC) = 2\pi a(a + b)\), значит:
\[
\frac{S_1}{S_2} = \frac{2\pi b(b + a)}{2\pi a(a + b)} = \frac{b}{a}
\]
Ответ: \(\frac{S_1}{S_2} = \frac{b}{a}\)
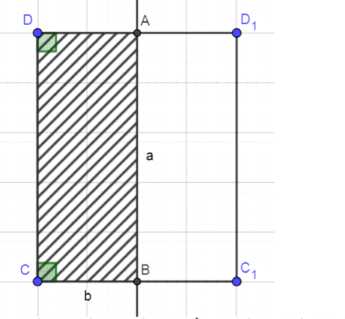
Дано: \(ABCD\) — прямоугольник; \(AB = a\); \(BC = b\).
Доказать: а) \(S_{1 \text{бок}} = S_{2 \text{бок}}\); Найти: б) \(\frac{S_1}{S_2} = ?\).
Решение:
а) Рассмотрим осевые сечения тел вращения.
Для первого тела вращения, осевое сечение — это прямоугольник \(ABCD\), вращающийся вокруг стороны \(AB\). Площадь боковой поверхности \(S_{1 \text{бок}}\) вычисляется как:
\[
S_{1 \text{бок}} = 2\pi \cdot BC \cdot AB = 2\pi \cdot b \cdot a
\]
Для второго тела вращения, осевое сечение — это прямоугольник \(ABCD\), вращающийся вокруг стороны \(BC\). Площадь боковой поверхности \(S_{2 \text{бок}}\) вычисляется как:
\[
S_{2 \text{бок}} = 2\pi \cdot AB \cdot BC = 2\pi \cdot a \cdot b
\]
Таким образом, \(S_{1 \text{бок}} = S_{2 \text{бок}}\), что и требовалось доказать.
б) Теперь найдем отношение полных поверхностей \(S_1\) и \(S_2\).
Площадь полной поверхности первого тела вращения \(S_1\) равна:
\[
S_1 = 2\pi \cdot BC(BC + AB) = 2\pi \cdot b(b + a)
\]
Площадь полной поверхности второго тела вращения \(S_2\) равна:
\[
S_2 = 2\pi \cdot AB(AB + BC) = 2\pi \cdot a(a + b)
\]
Теперь найдем отношение \(\frac{S_1}{S_2}\):
\[
\frac{S_1}{S_2} = \frac{2\pi \cdot b(b + a)}{2\pi \cdot a(a + b)} = \frac{b(b + a)}{a(a + b)} = \frac{b}{a}
\]
Таким образом, \(\frac{S_1}{S_2} = \frac{b}{a}\).
Ответ: \(\frac{S_1}{S_2} = \frac{b}{a}\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!