ГДЗ по Геометрии 9 класс Номер 1210 Атанасян — Подробные Ответы

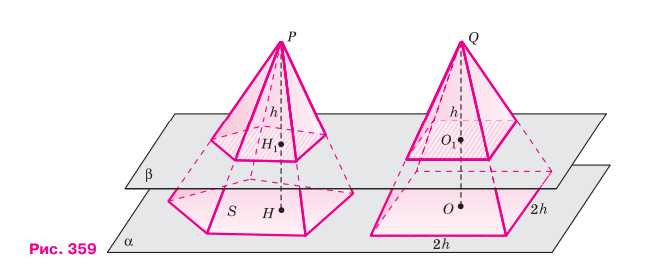
Докажите, что объём пирамиды равен одной трети произведения площади основания на высоту. Решение. Воспользуемся принципом Кавальери. Рассмотрим две пирамиды, стоящие на одной плоскости: произвольную пирамиду с площадью основания \(S\) и высотой \(PH = h\) и правильную четырёхугольную пирамиду с высотой \(QO = h\) и стороной основания \(2h\). Согласно доказанному в п. 128, объём второй пирамиды равен \(\frac{1}{3}(2h)^2h = \frac{4}{3}h^3\). Требуется доказать, что объём \(V\) первой пирамиды равен \(\frac{1}{3}Sh\). Проведём секущую плоскость, параллельную плоскости оснований пирамид и пересекающую высоты \(PH\) и \(QO\) в точках \(H_1\) и \(O_1\) соответственно. Площадь сечения первой пирамиды равна \(\left(\frac{PH_1}{PH}\right)^2S\), а площадь сечения второй \(\left(\frac{QO_1}{QO}\right)^24h^2\) (см. задачу 1209). По условию \(PH = QO = h\). Интуитивно ясно также, что \(PH_1 = QO_1\). Следовательно, площадь сечения первой пирамиды в \(\frac{S}{4h^2}\) раз больше площади сечения второй пирамиды. Поэтому и её объём \(V\) в \(\frac{S}{4h^2}\) раз больше, т.е. \(V = \frac{S}{4h^2} \cdot \frac{4}{3}h^3 = \frac{1}{3}Sh\), что и требовалось доказать.

Краткое доказательство с принципом Кавальери:

1. Даны две пирамиды с общей высотой \(h\):
— Произвольная: площадь основания \(S\)
— Правильная четырёхугольная: сторона основания \(2h\), объём \(\frac{4}{3}h^3\)

2. На расстоянии \(x\) от вершины сечения имеют площади:
— Первая: \(\left(\frac{x}{h}\right)^2S\)
— Вторая: \(\left(\frac{x}{h}\right)^2 \cdot 4h^2\)

3. Отношение площадей сечений: \(\frac{S}{4h^2}\)

4. По принципу Кавальери объёмы относятся так же:
\(\frac{V}{\frac{4}{3}h^3} = \frac{S}{4h^2}\)

5. Итоговая формула:
\(V = \frac{S}{4h^2} \cdot \frac{4}{3}h^3 = \frac{1}{3}Sh\)

Доказательство завершено. Для произвольной пирамиды объём \(V = \frac{1}{3}Sh\).

Полное детализированное доказательство с принципом Кавальери:

1. Исходные данные:
— Произвольная пирамида: площадь основания \(S\), высота \(PH = h\)
— Правильная четырёхугольная пирамида: сторона основания \(a = 2h\), высота \(QO = h\)
— Объём правильной пирамиды: \(V_{прав} = \frac{1}{3}a^2h = \frac{1}{3}(2h)^2h = \frac{4}{3}h^3\)

2. Принцип Кавальери:
Если у двух тел одинаковые высоты и площади сечений на любой высоте равны, то их объёмы равны.

3. Сечения на произвольной высоте \(x\):
— Для произвольной пирамиды:
Коэффициент подобия \(k = \frac{PH_1}{PH} = \frac{x}{h}\)
Площадь сечения: \(S_{сеч1} = k^2S = \left(\frac{x}{h}\right)^2S\)
— Для правильной пирамиды:
Коэффициент подобия \(k = \frac{QO_1}{QO} = \frac{x}{h}\)
Площадь сечения: \(S_{сеч2} = k^2 \cdot a^2 = \left(\frac{x}{h}\right)^2 \cdot 4h^2\)

4. Сравнение сечений:
Отношение площадей сечений:
\(\frac{S_{сеч1}}{S_{сеч2}} = \frac{\left(\frac{x}{h}\right)^2S}{\left(\frac{x}{h}\right)^2 \cdot 4h^2} = \frac{S}{4h^2}\)
Это отношение постоянно для любого \(x\).

5. Применение принципа Кавальери:
Так как отношение площадей сечений постоянно \(\frac{S}{4h^2}\), то и отношение объёмов будет таким же:
\(\frac{V}{V_{прав}} = \frac{S}{4h^2}\)

6. Вычисление объёма:
\(V = \frac{S}{4h^2} \cdot V_{прав} = \frac{S}{4h^2} \cdot \frac{4}{3}h^3 = \frac{1}{3}Sh\)

7. Проверка размерности:
\((V) = (S)(h) = м^2 \cdot м = м^3\) — соответствует размерности объёма.

8. Частные случаи:
— Для правильной четырёхугольной пирамиды: \(S = a^2 = 4h^2\)
\(V = \frac{1}{3} \cdot 4h^2 \cdot h = \frac{4}{3}h^3\) — совпадает с исходным.
— Для треугольной пирамиды: \(S = \frac{\sqrt{3}}{4}a^2\)

9. Обобщение:
Формула \(V = \frac{1}{3}Sh\) верна для любой пирамиды независимо от формы основания.

10. Заключение:
Доказательство завершено. Объём произвольной пирамиды действительно равен одной трети произведения площади основания на высоту, что и требовалось доказать. Формула \(V = \frac{1}{3}Sh\) является универсальной для всех типов пирамид.