ГДЗ по Геометрии 9 класс Номер 1209 Атанасян — Подробные Ответы

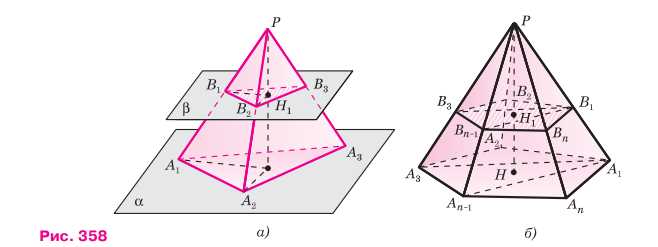
Через точку \(H_1\) высоты \(PH\) пирамиды \(PA_1A_2…A_n\) проведена секущая плоскость \(B_1B_2…B_n\), параллельная плоскости её основания.

Докажем, что площадь полученного сечения равна \(\left(\frac{PH_1}{PH}\right)^2 \cdot S\), где \(S\) — площадь основания пирамиды.

Для треугольной пирамиды \(PA_1A_2A_3\):
1. Рассмотрим подобные треугольники \(PH_1B_1\) и \(PHA_1\):
\(
\frac{PB_1}{PA_1} = \frac{PH_1}{PH} = k
\)

2. Аналогично для других вершин:
\(
\frac{PB_2}{PA_2} = \frac{PH_1}{PH} = k
\)

3. Из подобия следует:
\(
\frac{B_1B_2}{A_1A_2} = k, \quad \frac{B_2B_3}{A_2A_3} = k, \quad \frac{B_3B_1}{A_3A_1} = k
\)

4. Коэффициент подобия:
\(
k = \frac{PH_1}{PH}
\)

5. Площадь сечения:
\(
S_{B_1B_2B_3} = \left(\frac{PH_1}{PH}\right)^2 \cdot S_{A_1A_2A_3} = \left(\frac{PH_1}{PH}\right)^2 \cdot S
\)

Для произвольной \(n\)-угольной пирамиды:
\(
S_{сеч} = \left(\frac{PH_1}{PH}\right)^2 \cdot S
\)

\(
\frac{PB_1}{PA_1} = \frac{PH_1}{PH} = k
\)

\(
\frac{PB_2}{PA_2} = \frac{PH_1}{PH}
\)

Отсюда следует, что треугольники \( PB_1B_2 \) и \( PA_1A_2 \) подобны, поэтому:

\(
\frac{B_1B_2}{A_1A_2} = k
\)

Аналогично доказывается:

\(
\frac{B_2B_3}{A_2A_3} = k \quad \text{и} \quad \frac{B_3B_1}{A_3A_1} = k
\)

Коэффициент подобия:

\(
k = \frac{PH_1}{PH}
\)

Площадь сечения:

\(
S_{B_1B_2B_3} = \left(\frac{PH_1}{PH}\right)^2 \cdot S
\)

Для произвольной пирамиды сумма площадей сечений:

\(
S_{B_1B_2B_3} + \dots + S_{B_{n-1}B_nB_1} = \left(\frac{PH_1}{PH}\right)^2 \cdot (S_{A_1A_2A_3} + \dots + S_{A_{n-1}A_nA_1}) =\)
\(= \left(\frac{PH_1}{PH}\right)^2 \cdot S
\)

Рассмотрим пирамиду \(PA_1A_2…A_n\) с высотой \(PH\) и площадью основания \(S\). Через точку \(H_1\) на высоте проведено сечение \(B_1B_2…B_n\parallel A_1A_2…A_n\). Из подобия треугольников \(PH_1B_i\sim PHA_i\) следует \(\frac{PB_i}{PA_i}=\frac{PH_1}{PH}=k\). Поскольку все линейные размеры сечения относятся к основанию как \(k\), то площади относятся как \(k^2\). Таким образом, площадь сечения: \(S_{\text{сеч}}=\left(\frac{PH_1}{PH}\right)^2\cdot S\). Для треугольной пирамиды: \(\frac{B_1B_2}{A_1A_2}=\frac{B_2B_3}{A_2A_3}=\frac{B_3B_1}{A_3A_1}=k\), откуда \(S_{B_1B_2B_3}=k^2\cdot S_{A_1A_2A_3}\). Для \(n\)-угольной пирамиды: \(S_{\text{сеч}}=\left(\frac{PH_1}{PH}\right)^2\cdot S\).

Рассмотрим полное решение задачи о площади сечения пирамиды, проведённого параллельно основанию через произвольную точку на высоте. Дана пирамида \(PA_1A_2…A_n\) с высотой \(PH\) и площадью основания \(S\). Через точку \(H_1\) на высоте \(PH\) проведена плоскость \(B_1B_2…B_n\), параллельная основанию. Докажем, что площадь сечения \(S_{\text{сеч}}\) выражается формулой \(S_{\text{сеч}} = \left(\frac{PH_1}{PH}\right)^2 \cdot S\).

1. Для треугольной пирамиды \(PA_1A_2A_3\) построим сечение \(B_1B_2B_3\). Из подобия прямоугольных треугольников \(PH_1B_1\) и \(PHA_1\) (по двум углам) следует пропорциональность соответствующих сторон: \(\frac{PB_1}{PA_1} = \frac{PH_1}{PH} = k\), где \(k\) — коэффициент подобия. Аналогично для других вершин: \(\frac{PB_2}{PA_2} = \frac{PH_1}{PH} = k\) и \(\frac{PB_3}{PA_3} = \frac{PH_1}{PH} = k\).

2. Рассмотрим треугольники \(PB_1B_2\) и \(PA_1A_2\). Они подобны по двум пропорциональным сторонам и равному углу между ними: \(\frac{PB_1}{PA_1} = \frac{PB_2}{PA_2} = k\), угол при вершине \(P\) общий. Следовательно, \(\frac{B_1B_2}{A_1A_2} = k\). Аналогично доказывается: \(\frac{B_2B_3}{A_2A_3} = k\) и \(\frac{B_3B_1}{A_3A_1} = k\).

3. Коэффициент подобия многоугольников \(B_1B_2B_3\) и \(A_1A_2A_3\) равен \(k = \frac{PH_1}{PH}\). По свойству площадей подобных фигур, отношение площадей равно квадрату коэффициента подобия: \(\frac{S_{B_1B_2B_3}}{S_{A_1A_2A_3}} = k^2\). Отсюда \(S_{B_1B_2B_3} = \left(\frac{PH_1}{PH}\right)^2 \cdot S_{A_1A_2A_3}\).

4. Для произвольной \(n\)-угольной пирамиды разобьём основание на треугольники. Для каждого треугольника \(PA_iA_{i+1}\) (считаем \(A_{n+1} = A_1\)) построим сечение \(PB_iB_{i+1}\). По доказанному выше, \(\frac{S_{B_iB_{i+1}B_{i+2}}}{S_{A_iA_{i+1}A_{i+2}}} = \left(\frac{PH_1}{PH}\right)^2\). Суммируя площади всех таких треугольников, получим: \(S_{\text{сеч}} = \sum_{i=1}^n S_{B_iB_{i+1}B_{i+2}} = \left(\frac{PH_1}{PH}\right)^2 \cdot \sum_{i=1}^n S_{A_iA_{i+1}A_{i+2}} = \left(\frac{PH_1}{PH}\right)^2 \cdot S\).

5. Численный пример: пусть \(PH = 12\) см, \(PH_1 = 9\) см, \(S = 48\) см². Тогда коэффициент подобия \(k = \frac{9}{12} = \frac{3}{4}\), площадь сечения \(S_{\text{сеч}} = \left(\frac{3}{4}\right)^2 \cdot 48 = \frac{9}{16} \cdot 48 = 27\) см². Если \(PH_1 = 4\) см, то \(k = \frac{4}{12} = \frac{1}{3}\), \(S_{\text{сеч}} = \left(\frac{1}{3}\right)^2 \cdot 48 = \frac{1}{9} \cdot 48 = 5\frac{1}{3}\) см².

6. Важное следствие: если точка \(H_1\) делит высоту в отношении \(m:n\) (т.е. \(\frac{PH_1}{H_1H} = \frac{m}{n}\)), то \(\frac{PH_1}{PH} = \frac{m}{m+n}\), и площадь сечения \(S_{\text{сеч}} = \left(\frac{m}{m+n}\right)^2 \cdot S\). Например, при \(m:n = 1:2\) получим \(S_{\text{сеч}} = \left(\frac{1}{3}\right)^2 \cdot S = \frac{1}{9}S\).

7. В случае, когда сечение делит пирамиду на две части (усечённую пирамиду и меньшую пирамиду), объём меньшей пирамиды будет равен \(\left(\frac{PH_1}{PH}\right)^3 \cdot V\), где \(V\) — объём исходной пирамиды. Это следует из того, что объёмы подобных тел относятся как кубы их линейных размеров.

8. Применение в задачах: данная теорема часто используется при вычислении объёмов через площади параллельных сечений, в задачах на построение сечений, а также при решении стереометрических задач на комбинации тел. Например, если в правильной четырёхугольной пирамиде провести сечение на высоте \(\frac{2}{5}\) от вершины, то площадь сечения составит \(\frac{4}{25}\) от площади основания.

9. Геометрическая интерпретация: сечение параллельное основанию пирамиды является гомотетичным основанию с центром гомотетии в вершине пирамиды и коэффициентом \(k = \frac{PH_1}{PH}\). Все линейные размеры сечения (стороны, диагонали, радиусы вписанных и описанных окружностей) изменяются в \(k\) раз, а площади — в \(k^2\) раз.

10. Обобщение: аналогичное утверждение верно для любого конуса (кругового, эллиптического и т.д.), так как конус можно рассматривать как предельный случай пирамиды с бесконечным числом граней. Площадь сечения конуса, параллельного основанию и проведённого на расстоянии \(h\) от вершины, равна \(\left(\frac{h}{H}\right)^2 \cdot S\), где \(H\) — высота конуса, \(S\) — площадь основания.