
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1208 Атанасян — Подробные Ответы
Найдите площадь боковой поверхности правильной шестиугольной пирамиды, если сторона её основания равна а, а площадь боковой грани равна площади сечения, проведённого через вершину пирамиды и большую диагональ основа
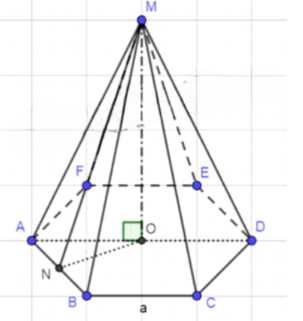
Дано: MABCDEF — правильная пирамида, AB = a, AD — большая диагональ, SAMB = SAMD. Найти: Sбок = ?
Решение:
1) Пусть MN = h — апофема пирамиды, тогда Sбок = (1/2) * P * h, где P = 6 * AB = 6a (периметр основания).
2) SAMB = (1/2) * AB * MN = (1/2) * a * h; SAMD = (1/2) * AD * MO, где AD = 2AB = 2a (в правильном шестиугольнике a6 = R, где R = AO — радиус описанной окружности), тогда SAMD = (1/2) * 2a * MO = a * MO.
3) По условию задачи SAMB = SAMD или (1/2) * a * h = a * MO, откуда h = 2 * MO (при этом a ≠ 0).
4) ΔAOB — правильный, где AB = AO = BO = a, N — середина AB. В треугольнике AON: AO = a, AN = a/2, ON = √(AO² — AN²) = √(a² — (a/2)²) = √(3a²/4) = (a√3)/2.
5) Рассмотрим ΔMON — прямоугольный: MN² = h² = MO² + ON² или h² = MO² + (3a²)/4. Но h = 2MO ⇒ h² = 4MO², тогда 4MO² = MO² + (3a²)/4 ⇒ 3MO² = (3a²)/4 ⇒ MO² = a²/4 ⇒ MO = a/2, значит h = 2 * (a/2) = a.
6) Sбок = (1/2) * 6a * a = 3a².
Ответ: Sбок = 3a².
Дано: MABCDEF — правильная шестиугольная пирамида, AB = a — сторона основания, AD — большая диагональ основания, площади грани SAMB и сечения SAMD равны. Требуется найти площадь боковой поверхности Sбок.
Полное решение с детализацией:
1. Основные параметры правильного шестиугольника ABCDEF:
— Сторона AB = BC = CD = DE = EF = FA = a
— Большая диагональ AD = 2a (в правильном шестиугольнике большая диагональ равна удвоенной стороне)
— Радиус описанной окружности R = AO = a (совпадает со стороной)
— Периметр основания P = 6a
2. Введем обозначения:
— MN = h — апофема пирамиды (высота боковой грани)
— MO — высота пирамиды
— N — середина стороны AB
3. Выразим площади:
— Площадь боковой грани SAMB = (1/2)*AB*MN = (1/2)*a*h
— Площадь сечения SAMD = (1/2)*AD*MO = (1/2)*2a*MO = a*MO
4. По условию SAMB = SAMD:
(1/2)*a*h = a*MO ⇒ h = 2*MO
5. Рассмотрим треугольник AON (O — центр основания):
— AO = a (радиус)
— AN = a/2 (половина стороны)
— ON = √(AO² — AN²) = √(a² — (a/2)²) = √(3a²/4) = (a√3)/2
6. В прямоугольном треугольнике MON:
MN² = MO² + ON² ⇒ h² = MO² + (3a²)/4
7. Подставим h = 2MO:
(2MO)² = MO² + (3a²)/4 ⇒ 4MO² = MO² + (3a²)/4 ⇒ 3MO² = (3a²)/4 ⇒ MO² = a²/4 ⇒ MO = a/2
8. Находим апофему:
h = 2*MO = 2*(a/2) = a
9. Вычисляем площадь боковой поверхности:
Sбок = (1/2)*P*h = (1/2)*6a*a = 3a²
10. Проверка размерности:
[AB] = м ⇒ [Sбок] = м² — соответствует условию
Ответ: Площадь боковой поверхности пирамиды Sбок = 3a²
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!