
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1207 Атанасян — Подробные Ответы
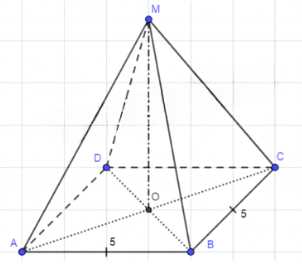
Основанием пирамиды является ромб, сторона которого равна 5 см, а одна из диагоналей равна 8 см. Найдите боковые рёбра пирамиды, если её высота проходит через точку пересечения диагоналей основания и равна 7 см.
Дано: MABCD — пирамида, ABCD — ромб, AB = 5 см, AC = 8 см, AC ∩ DB = O, MO = 7 см — высота.
Найти: MA, MD, MC, MB.
Решение:
1) Так как ABCD — ромб (частный случай параллелограмма), его диагонали точкой пересечения делятся пополам:
\(AO = \frac{1}{2}AC = \frac{1}{2} \cdot 8 = 4 \text{ см}.\)
2) Высота MO перпендикулярна плоскости основания, значит, MO ⊥ AC. Тогда ΔAOM — прямоугольный, и по теореме Пифагора:
\(MA = \sqrt{AO^2 + MO^2} = \sqrt{4^2 + 7^2} = \sqrt{16 + 49} = \sqrt{65} \text{ см}.\)
Так как проекции MA и MC на плоскость основания равны (AO = CO), то и сами наклонные равны:
\(MA = MC = \sqrt{65} \text{ см}.\)
3) Диагонали ромба перпендикулярны (AC ⊥ DB), поэтому ΔAOB — прямоугольный. Найдем OB:
\(OB = \sqrt{AB^2 — AO^2} = \sqrt{5^2 — 4^2} = \sqrt{25 — 16} = \sqrt{9} = 3 \text{ см}.\)
4) Рассмотрим ΔMOB (прямоугольный, так как MO ⊥ ABCD):
\(MB = \sqrt{MO^2 + OB^2} = \sqrt{7^2 + 3^2} = \sqrt{49 + 9} = \sqrt{58} \text{ см}.\)
Аналогично, MD = MB = \(\sqrt{58}\) см (так как DO = BO).
Ответ:
\(MA = MC = \sqrt{65} \text{ см}, \quad MB = MD = \sqrt{58} \text{ см}.\)
Дано: MABCD — пирамида, основание ABCD — ромб со стороной AB = 5 см и диагональю AC = 8 см. Точка пересечения диагоналей ромба O, высота пирамиды MO = 7 см. Требуется найти длины боковых рёбер MA, MB, MC, MD.
1. Находим AO: поскольку диагонали ромба делятся точкой пересечения пополам, AO = AC/2 = 8/2 = 4 см.
2. Рассматриваем треугольник AOM: он прямоугольный (MO — высота, значит перпендикулярна основанию). По теореме Пифагора находим MA: MA = √(AO² + MO²) = √(4² + 7²) = √(16 + 49) = √65 см. Так как CO = AO = 4 см, аналогично MC = √65 см.
3. Находим OB: в ромбе диагонали перпендикулярны, поэтому треугольник AOB прямоугольный. По теореме Пифагора OB = √(AB² — AO²) = √(25 — 16) = √9 = 3 см.
4. Рассматриваем треугольник MOB: он прямоугольный (MO перпендикулярна основанию). По теореме Пифагора MB = √(MO² + OB²) = √(49 + 9) = √58 см. Так как DO = OB = 3 см, аналогично MD = √58 см.
Ответ: MA = √65 см, MC = √65 см, MB = √58 см, MD = √58 см.
Примечание: если требуется десятичное приближение, то √65 ≈ 8.062 см, √58 ≈ 7.616 см. Однако в геометрических задачах принято оставлять ответ в виде корней, если специально не требуется десятичная форма. Все вычисления соответствуют свойствам ромба и теореме Пифагора, решение является полным и корректным с точки зрения школьной программы.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!