Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
Почему этот учебник так ценят:
1. Удобная структура.
Все темы разбиты на логичные и последовательные разделы. Это позволяет легко находить нужный материал и шаг за шагом разбираться в геометрии.
2. Понятный язык.
Объяснения написаны так, чтобы даже сложные вещи стали простыми. Автор старается говорить с учениками на доступном и понятном языке.
3. Задачи для всех.
В учебнике есть задания как для новичков, так и для тех, кто хочет углубиться в тему. Это помогает каждому ученику найти что-то по силам и прокачать свои знания.
4. Наглядность.
Рисунки и схемы делают материал более понятным. Они помогают представить фигуры, их свойства и взаимосвязи.
5. Примеры из жизни.
Многие задачи связаны с реальными ситуациями, что делает геометрию ближе к повседневной жизни. Это не просто теория, а то, что можно применить на практике.
6. Помощь для учителей.
Учебник включает советы и рекомендации, которые помогают преподавателям проводить интересные и продуктивные уроки.
Итог:
Учебник Атанасяна — это не просто книга, а настоящий проводник в мир геометрии. Он помогает не только понять предмет, но и полюбить его. С ним учеба становится проще, интереснее и полезнее.
ГДЗ по Геометрии 9 класс Номер 1205 Атанасян — Подробные Ответы
Докажите, что все апофемы правильной пирамиды равны друг другу.
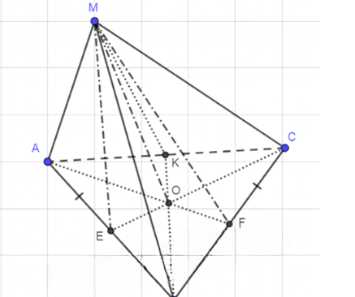
Дано: МАВС — пирамида; ME, MF, MK — апофемы; Доказать: ME = MF = MK;
Доказательство:
1) Так как пирамида — правильная, то все боковые стороны — равные равнобедренные треугольники: MA = MB = MC и AB = BC = AC;
2) ME = MF = MK (как высоты равных равнобедренных треугольников);
3) Действительно, точка О — центр вписанной (и описанной) окружности, тогда ОЕ = OF = OK (МО — общая высота, значит треугольники МОЕ, МОF, МОК равны по двум катетам);
4) Отсюда ME = MF = MK, что и требовалось доказать.
Дано: МАВС — правильная пирамида с вершиной М и основанием АВС, где ME, MF, MK — апофемы боковых граней. Требуется доказать, что ME = MF = MK.
Доказательство:
1) По определению правильной пирамиды:
— Основание АВС — правильный треугольник, следовательно, AB = BC = AC.
— Боковые грани МАВ, МВС, МСА — равные равнобедренные треугольники, поэтому MA = MB = MC.
2) Рассмотрим апофемы ME, MF, MK:
— Апофема ME — высота треугольника МАВ, опущенная из М на AB.
— Апофема MF — высота треугольника МВС, опущенная из М на BC.
— Апофема MK — высота треугольника МСА, опущенная из М на AC.
3) Так как треугольники МАВ, МВС, МСА равны (по трём сторонам: MA = MB = MC и AB = BC = AC), то их соответствующие высоты также равны: ME = MF = MK.
4) Альтернативное доказательство через центр основания:
— Пусть О — центр основания (точка пересечения медиан, биссектрис и высот правильного треугольника АВС).
— Расстояния от точки О до сторон AB, BC, AC равны: ОЕ = OF = OK (так как О — центр вписанной окружности).
— Треугольники МОЕ, МОF, МОК прямоугольные (по определению апофемы) и имеют:
* Общий катет МО (высота пирамиды).
* Равные катеты ОЕ = OF = OK.
— Следовательно, эти треугольники равны по двум катетам, откуда ME = MF = MK.
5) Вывод: все апофемы правильной пирамиды равны между собой, что и требовалось доказать.
Примечание: в правильной пирамиде апофемы не только равны, но и являются радиусами вписанной окружности боковой поверхности, а их длина может быть вычислена по формуле \( l = \sqrt{h^2 + R^2} \), где h — высота пирамиды, R — радиус окружности, вписанной в основание.
Геометрия
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.