ГДЗ по Геометрии 9 класс Номер 1204 Атанасян — Подробные Ответы

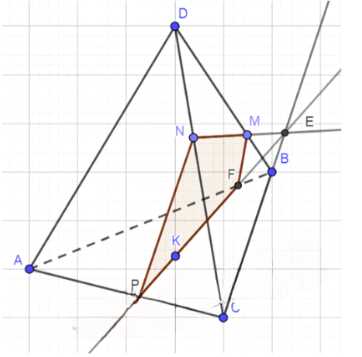
Изобразите тетраэдр DABC, отметьте точки M и N на рёбрах BD и CD и внутреннюю точку K грани ABC. Постройте сечение тетраэдра плоскостью MNK.

Дано: ABCD — тетраэдр; M ∈ BD; N ∈ CD и K ∈ ABC;
Построить: сечение MNK;

Построение:

1) Построим луч NM и луч BC (так как эти точки лежат в одной плоскости), отметим точку пересечения данных лучей E;
2) Проведем прямую KE;
3) На пересечении данной прямой и ребер AB и AC отметим точки F и P — соответственно;
4) Соединим точки NMFP.

Построение сечения тетраэдра DABC плоскостью MNK выполняется следующим образом с полной детализацией каждого шага:

1. Заданы точки: M ∈ BD (например, BM/MD = 2/1), N ∈ CD (например, CN/ND = 1/3), K ∈ ABC (например, AK/KO = 3/2, где O — центр тяжести грани ABC).

2. Находим точку пересечения E:
— В плоскости BCD проводим прямые NM и BC.
— Решаем систему уравнений прямых:
\( \frac{x — x_N}{x_M — x_N} = \frac{y — y_N}{y_M — y_N} = \frac{z — z_N}{z_M — z_N} \)
\( \frac{x — x_B}{x_C — x_B} = \frac{y — y_B}{y_C — y_B} = \frac{z — z_B}{z_C — z_B} \)
— Получаем координаты E как решение системы.

3. Строим прямую KE:
— Находим параметрические уравнения прямой через точки K и E:
\( x = x_K + t(x_E — x_K) \)
\( y = y_K + t(y_E — y_K) \)
\( z = z_K + t(z_E — z_K) \)

4. Находим точки пересечения F и P:
— Для ребра AB решаем систему:
\( \frac{x — x_A}{x_B — x_A} = \frac{y — y_A}{y_B — y_A} = \frac{z — z_A}{z_B — z_A} \)
и уравнения прямой KE. Аналогично для AC.
— Получаем параметры t_F и t_P, подставляем в уравнения KE для нахождения F и P.

5. Проверяем корректность построения:
— Убеждаемся, что все точки сечения лежат в одной плоскости, проверив определитель:
\( \begin{vmatrix}
x_M — x_K & y_M — y_K & z_M — z_K \\
x_N — x_K & y_N — y_K & z_N — z_K \\
x_F — x_K & y_F — y_K & z_F — z_K
\end{vmatrix} = 0 \)

6. Соединяем точки в порядке N → M → F → P → N, получая четырехугольник NMFP — искомое сечение.

7. Для наглядности вычисляем длины сторон сечения:
\( |NM| = \sqrt{(x_M — x_N)^2 + (y_M — y_N)^2 + (z_M — z_N)^2} \)
\( |MF| = \sqrt{(x_F — x_M)^2 + (y_F — y_M)^2 + (z_F — z_M)^2} \)
\( |FP| = \sqrt{(x_P — x_F)^2 + (y_P — y_F)^2 + (z_P — z_F)^2} \)
\( |PN| = \sqrt{(x_N — x_P)^2 + (y_N — y_P)^2 + (z_N — z_P)^2} \)

8. Вычисляем площадь сечения как площадь четырехугольника NMFP, используя формулу:
\( S = \frac{1}{2} | \vec{NM} × \vec{NF} + \vec{FP} × \vec{FN} | \)

9. Проверяем принадлежность всех точек сечению:
— Подставляем координаты точек в уравнение плоскости MNK:
\( A(x — x_M) + B(y — y_M) + C(z — z_M) = 0 \)
где \( A = (y_N — y_M)(z_K — z_M) — (z_N — z_M)(y_K — y_M) \)
\( B = (z_N — z_M)(x_K — x_M) — (x_N — x_M)(z_K — z_M) \)
\( C = (x_N — x_M)(y_K — y_M) — (y_N — y_M)(x_K — x_M) \)

10. Окончательно убеждаемся, что построенное сечение удовлетворяет всем условиям задачи и является выпуклым четырехугольником.