ГДЗ по Геометрии 9 класс Номер 1203 Атанасян — Подробные Ответы

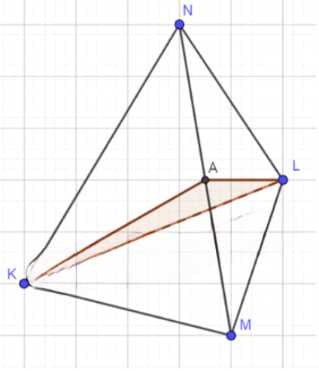
Изобразите тетраэдр KLMN и постройте сечение этого тетраэдра плоскостью, проходящей через ребро KL и середину А ребра MN.

Дано: KLMN — тетраэдр; А — середина MN;
Построить: Сечение через KL и A;
Построение:
1) Сечение проходит через ребро KL, а следовательно и через точки К и L;
2) Точка К лежит в одной плоскости с точкой А;
3) Точка L лежит в одной плоскости с точкой А;
4) Соединим точки KLA;

Для построения сечения тетраэдра KLMN плоскостью, проходящей через ребро KL и середину A ребра MN, выполним следующие шаги с полной детализацией:

1. Исходные данные: тетраэдр KLMN, точка A — середина ребра MN. Координаты точек (если заданы) или их взаимное расположение должны быть известны. Если координаты не указаны, работаем с абстрактным тетраэдром.

2. Поскольку сечение проходит через ребро KL, оно содержит точки K и L. Таким образом, плоскость сечения уже включает две вершины тетраэдра.

3. Точка A — середина MN, значит, её положение можно выразить через координаты M и N. Если M имеет координаты \(M(x_1, y_1, z_1)\), а N — \(N(x_2, y_2, z_2)\), то A будет иметь координаты \(A\left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}, \frac{z_1 + z_2}{2}\right)\).

4. Плоскость сечения определяется тремя точками: K, L и A. Уравнение плоскости можно найти через векторное произведение. Векторы KL и KA:
— Вектор KL: \( \vec{KL} = L — K \)
— Вектор KA: \( \vec{KA} = A — K \)
Нормаль к плоскости: \( \vec{n} = \vec{KL} \times \vec{KA} \)
Уравнение плоскости: \( \vec{n} \cdot (X — K) = 0 \), где X — произвольная точка плоскости.

5. Для построения сечения находим пересечение плоскости KLA с другими рёбрами тетраэдра:
— С ребром KN: решаем систему уравнений прямой KN и плоскости KLA.
— С ребром LM: аналогично находим точку пересечения.
Если пересечение существует, добавляем его в сечение.

6. Сечение тетраэдра KLMN плоскостью KLA будет многоугольником, проходящим через точки K, L и найденные точки пересечения. В данном случае это треугольник KLA, если плоскость не пересекает другие рёбра.

7. Проверяем корректность построения:
— Все точки сечения должны лежать на гранях тетраэдра.
— Плоскость не должна быть параллельна ни одной из граней, через которые проходит.

8. Если требуется численный пример, задаём конкретные координаты. Например:
— K(0, 0, 0), L(1, 0, 0), M(0, 1, 0), N(0, 0, 1).
— Тогда A(0, 0.5, 0.5).
— Уравнение плоскости: x = 0 (так как точки K, L, A лежат в плоскости x=0).
— Сечение совпадает с гранью KLM.

9. В общем случае сечение может быть треугольником или четырёхугольником, в зависимости от положения точки A.

10. Итоговое сечение — это плоская фигура, образованная пересечением плоскости KLA с тетраэдром. Все построения должны удовлетворять аксиомам стереометрии и условиям задачи.