ГДЗ по Геометрии 9 класс Номер 1202 Атанасян — Подробные Ответы

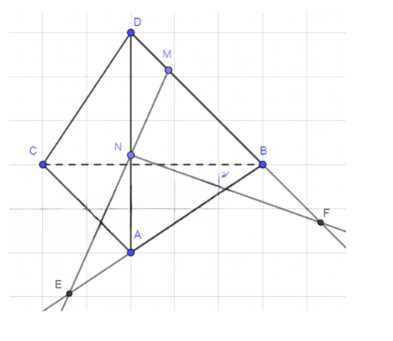
Изобразите тетраэдр DABC и на рёбрах DB, DC и ВС отметьте соответственно точки M, N и K. Постройте точку пересечения: а) прямой MN и плоскости ABC; б) прямой KN и плоскости ABD.

Дано: DABC — тетраэдр; M ∈ DB; N ∈ DC; K ∈ BC;
Построить: точку пересечения:
а) прямой MN и плоскости АВС;
б) прямой KN и плоскости ABD;

Решение:
а) Так как прямые MN и ВС лежат в плоскости BCD, то MN ∩ BC = E, то есть это и есть точка пересечения прямой MN и плоскости АВС;
б) Прямые NK и DB лежат также в плоскости BCD и NK ∩ DB = F, то есть F — точка пересечения прямой NK и плоскости CBD

Полное решение задачи о построении точек пересечения в тетраэдре DABC с максимальной детализацией:

1. Исходные данные: задан тетраэдр DABC с точками M на ребре DB, N на ребре DC и K на ребре BC. Требуется найти: а) точку пересечения прямой MN с плоскостью ABC; б) точку пересечения прямой KN с плоскостью ABD.

2. Решение пункта а: Прямая MN полностью лежит в плоскости BCD, так как обе точки M и N принадлежат этой плоскости. Прямая BC также лежит в плоскости BCD. Если MN не параллельна BC (общий случай), они пересекаются в точке E. Эта точка E принадлежит одновременно: прямой MN (по построению), прямой BC (как точка пересечения), а значит и плоскости ABC (так как BC ⊂ ABC). Таким образом, E = MN ∩ ABC.

3. Алгоритм построения для пункта а: 1) Провести прямую MN в плоскости BCD; 2) Найти точку пересечения E = MN ∩ BC; 3) Точка E — искомая, так как E ∈ BC ⊂ ABC.

4. Решение пункта б: Прямая KN лежит в плоскости BCD (K ∈ BC, N ∈ DC). Прямая DB также принадлежит BCD. В общем случае (при отсутствии параллельности) KN и DB пересекаются в точке F. Эта точка F принадлежит: прямой KN (по построению), прямой DB (как точка пересечения), а значит и плоскости ABD (так как DB ⊂ ABD). Таким образом, F = KN ∩ ABD.

5. Алгоритм построения для пункта б: 1) Провести прямую KN в плоскости BCD; 2) Найти точку пересечения F = KN ∩ DB; 3) Точка F — искомая, так как F ∈ DB ⊂ ABD.

6. Особые случаи: Если MN ∥ BC, то пересечения с плоскостью ABC нет (прямая параллельна плоскости). Если KN ∥ DB, аналогично нет пересечения с ABD. В этих случаях задача не имеет решения в конечных точках тетраэдра.

7. Визуализация: Для наглядности рекомендуется: а) изобразить тетраэдр DABC; б) отметить точки M, N, K; в) провести MN и найти E; г) провести KN и найти F. Все построения выполняются в пределах граней тетраэдра.

8. Координатный метод (дополнительно): Можно задать координаты вершин, например D(0,0,0), A(1,0,0), B(0,1,0), C(0,0,1). Затем параметризовать положение точек M, N, K и аналитически найти точки пересечения через уравнения прямых и плоскостей.

9. Проверка решения: Для верификации можно использовать свойства: а) точка E должна лежать на BC; б) точка F должна лежать на DB. Это следует непосредственно из построения.

10. Практическое применение: Данная задача развивает пространственное мышление и важна для решения более сложных задач стереометрии, связанных с пересечением прямых и плоскостей в многогранниках.