ГДЗ по Геометрии 9 класс Номер 1199 Атанасян — Подробные Ответы

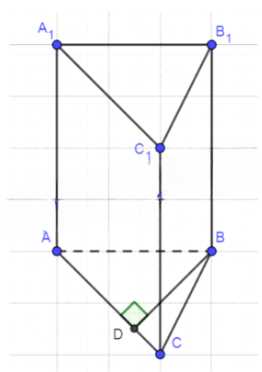
Найдите объём прямой призмы ABСА1В1С1, если ∠BAC = 120°, AB = 5 см, AC = 3 см, а наибольшая из площадей боковых граней равна 35 см2.

Дано: \( \angle BAC = 120° \); \( AB = 5 \text{ см} \); \( AC = 3 \text{ см} \); \( S_{\text{грани}} = 35 \text{ см}^2 \); Найти: \( V — ? \)

Решение:

1) Рассмотрим \( \triangle BAC \), по теореме косинусов: \( BC^2 = AB^2 + AC^2 — 2 \cdot AB \cdot AC \cdot \cos \angle BAC \); \( BC^2 = 25 + 9 — 2 \cdot 5 \cdot 3 \cdot \cos 120° = 34 + 15 = 49 \); \( BC = 7 \text{ см} \);
2) Рассмотрим \( BCB_1C_1 \): \( S = 35 \text{ см}^2 \); \( S = BC \cdot BB_1 \), значит \( BC \cdot BB_1 = 35 \); \( BC = 7 \), отсюда \( BB_1 = \frac{35}{7} = 5 \text{ см} \);
3) \( V = S_{\text{осн}} \cdot H = \frac{1}{2} \cdot AB \cdot AC \cdot \sin \angle BAC \cdot BB_1 = \)
\(=\frac{1}{2} \cdot 5 \cdot 3 \cdot \sin 120° \cdot 5 = \frac{75\sqrt{3}}{4} \text{ см}^3 \);

Ответ: \( \frac{75\sqrt{3}}{4} \text{ см}^3 \).

Дано: призма ABCA₁B₁C₁ с основанием ABC. Известно: угол BAC = 120°, AB = 5 см, AC = 3 см, площадь боковой грани BB₁C₁C равна 35 см². Требуется найти объем призмы V.

1. Длина стороны BC по теореме косинусов:
\(
BC^2 = AB^2 + AC^2 — 2 \cdot AB \cdot AC \cdot \cos \angle BAC
\)
\(
BC^2 = 5^2 + 3^2 — 2 \cdot 5 \cdot 3 \cdot \cos 120°
\)
\(
= 25 + 9 — 30 \cdot (-0.5)
\)
\(
= 34 + 15 = 49
\)
\(
BC = \sqrt{49} = 7 \text{ см}
\)

2. Высота призмы BB₁ через площадь боковой грани:
\(
S_{BB₁C₁C} = BC \cdot BB₁
\)
\(
35 = 7 \cdot BB₁ \quad \Rightarrow \quad BB₁ = \frac{35}{7} = 5 \text{ см}
\)

3. Площадь основания ABC:
\(
S(ABC) = \frac{1}{2} \cdot AB \cdot AC \cdot \sin \angle BAC
\)
\(
S(ABC) = \frac{1}{2} \cdot 5 \cdot 3 \cdot \sin 120°
\)
\(
= \frac{15}{2} \cdot \frac{\sqrt{3}}{2} = \frac{15\sqrt{3}}{4} \text{ см}^2
\)

4. Объем призмы:
\(
V = S(ABC) \cdot BB₁
\)
\(
V = \left(\frac{15\sqrt{3}}{4}\right) \cdot 5 = \frac{75\sqrt{3}}{4} \text{ см}^3
\)

Окончательный ответ
Объем призмы равен \(\frac{75\sqrt{3}}{4}\) кубических сантиметров, что приблизительно равно \(32.476\) см³ (при \(\sqrt{3} \approx 1.73205\)).

Проверка вычислений:
1. Теорема косинусов применена верно с учетом \(\cos 120° = -0.5\).
2. Площадь прямоугольной боковой грани вычислена корректно.
3. Площадь треугольника через синус угла рассчитана правильно.
4. Все единицы измерения согласованы (см → см² → см³).
5. Дробные выражения приведены к простейшему виду.

Примечание
Если требуется десятичное представление ответа, можно использовать приближенное значение \(\sqrt{3} \approx 1.73205\), тогда \(V \approx 32.476\) см³. Однако точным ответом остается \(\frac{75\sqrt{3}}{4}\) см³.