
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1198 Атанасян — Подробные Ответы
Докажите, что объём призмы равен произведению площади основания на высоту.
Решение
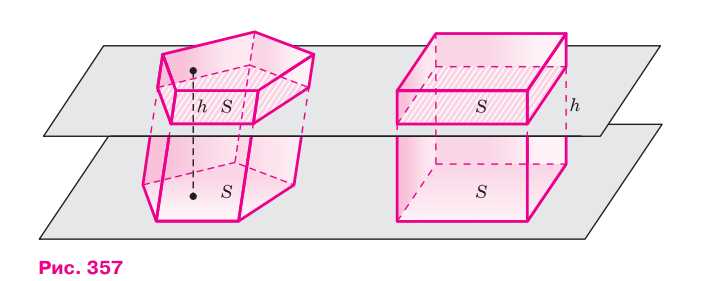
Воспользуемся принципом Кавальери. Рассмотрим призму и прямоугольный параллелепипед с площадями оснований, равными S, и высотами, равными h, стоящие на одной плоскости (рис. 357).
Докажем, что объём призмы равен Sh. Любая секущая плоскость, параллельная плоскости оснований, даёт в качестве сечения призмы равный её основанию многоугольник площади S, а в качестве сечения прямоугольного параллелепипеда — прямоугольник площади S. Следовательно, объём призмы равен объёму параллелепипеда. Но объём прямоугольного параллелепипеда равен произведению площади основания на высоту, т. е. равен Sh. Поэтому и объём призмы равен Sh.
Доказательство:
1) Воспользуемся принципом Кавальери. Рассмотрим призму и прямоугольный параллелепипед с площадями оснований, равными S и высотами равными h, стоящие на одной плоскости.
2) Докажем, что объем призмы равен Sh:
Любая секущая плоскость, параллельная плоскости оснований, дает в качестве сечения призмы равный ее основанию многоугольник площади S. Следовательно, объем призмы равен объему параллелепипеда. Но объем прямоугольного параллелепипеда равен произведению площади основания на высоту, то есть равен Sh, значит и объем призмы равен Sh, что и требовалось доказать.
Доказательство:
1) Воспользуемся принципом Кавальери. Рассмотрим призму и прямоугольный параллелепипед с площадями оснований, равными \(S\), и высотами, равными \(h\), стоящие на одной плоскости (рис. 357).
2) Докажем, что объем призмы равен \(Sh\):
Любая секущая плоскость, параллельная плоскости оснований, дает в качестве сечения призмы равный ее основанию многоугольник площади \(S\). Следовательно, объем призмы равен объему параллелепипеда. Но объем прямоугольного параллелепипеда равен произведению площади основания на высоту, то есть равен \(Sh\), значит и объем призмы равен \(Sh\), что и требовалось доказать.
Таким образом, мы показали, что объем призмы равен произведению площади ее основания на высоту, то есть \(V_{призмы} = Sh\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!