
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1197 Атанасян — Подробные Ответы
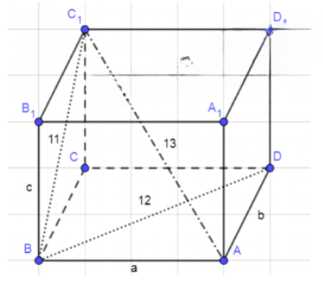
Найдите объём прямоугольного параллелепипеда ABCDA1B1C1D1, если AC1 = 13 см, BD = 12 см и BC1 = 11 см.
Рассмотрим параллелепипед с измерениями \( AB = a \), \( AD = b \), \( BB_1 = c \).
1. По теореме Пифагора:
\( a^2 + b^2 = 12^2 = 144 \).
2. Диагональ \( A_1C = d = 13 \) см:
\( d^2 = a^2 + b^2 + c^2 \)
\( 13^2 = 144 + c^2 \)
\( 169 = 144 + c^2 \)
\( c^2 = 25 \)
\( c = 5 \) см.
3. Рассмотрим треугольник \( \Delta BSC_1 \):
\( b^2 + c^2 = 11^2 \)
\( b^2 + 5^2 = 121 \)
\( b^2 + 25 = 121 \)
\( b^2 = 96 \)
\( b = 4\sqrt{6} \) см.
4. Найдем \( a \):
\( a^2 = 144 — 96 = 48 \)
\( a = 4\sqrt{3} \) см.
5. Объем \( V \):
\( V = abc = (4\sqrt{3}) \cdot (4\sqrt{6}) \cdot 5 \)
\( V = 80\sqrt{18} = 240\sqrt{2} \) см³.
Ответ: \( 240\sqrt{2} \) см³.
Рассмотрим параллелепипед с измерениями \( AB = a \), \( AD = b \), \( BB_1 = c \).
1. По теореме Пифагора для прямоугольного треугольника \( ABAD \) имеем:
\(
a^2 + b^2 = 12^2 = 144.
\)
2. Дана диагональ параллелепипеда \( A_1C = d = 13 \) см. По формуле для диагонали параллелепипеда:
\(
d^2 = a^2 + b^2 + c^2.
\)
Подставляя известные значения, получаем:
\(
13^2 = a^2 + b^2 + c^2 \quad \Rightarrow \quad 169 = 144 + c^2.
\)
Отсюда находим \( c^2 \):
\(
c^2 = 169 — 144 = 25 \quad \Rightarrow \quad c = 5 \text{ см}.
\)
3. Рассмотрим треугольник \( \Delta BSC_1 \), который также является прямоугольным:
\(
BC^2 + (CC_1)^2 = (BC_1)^2.
\)
Здесь \( BC = AD = b \), \( CC_1 = BB_1 = c \), \( BC_1 = 11 \) см. Подставим известные значения:
\(
b^2 + c^2 = 11^2 \quad \Rightarrow \quad b^2 + 5^2 = 121 \quad \Rightarrow \quad b^2 + 25 = 121.
\)
Отсюда находим \( b^2 \):
\(
b^2 = 121 — 25 = 96 \quad \Rightarrow \quad b = \sqrt{96} = 4\sqrt{6} \text{ см}.
\)
4. Теперь мы можем найти \( a \):
\(
a^2 = 144 — b^2 = 144 — 96 = 48 \quad \Rightarrow \quad a = \sqrt{48} = 4\sqrt{3} \text{ см}.
\)
5. Теперь можем вычислить объем \( V \) параллелепипеда:
\(
V = abc = (4\sqrt{3}) \cdot (4\sqrt{6}) \cdot 5.
\)
Упростим выражение:
\(
V = 4 \cdot 4 \cdot 5 \cdot \sqrt{3 \cdot 6} = 80 \cdot \sqrt{18} = 80 \cdot 3\sqrt{2} = 240\sqrt{2} \text{ см}^3.
\)
Таким образом, объем параллелепипеда равен \( 240\sqrt{2} \) см³.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!