ГДЗ по Геометрии 9 класс Номер 1196 Атанасян — Подробные Ответы

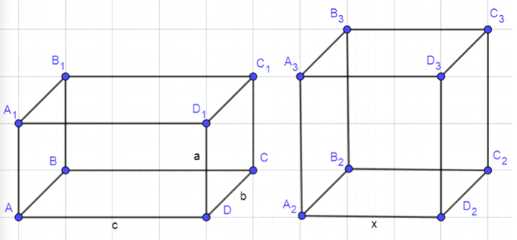
Измерения прямоугольного параллелепипеда равны 8 см, 12 см и 18 см. Найдите ребро куба, объём которого равен объёму этого параллелепипеда.

Решение:

1) Пусть х — ребро куба, тогда \(V_{куба} = x^3\)
2) \(V_{парал} = a \cdot b \cdot c\), тогда \(x^3 = abc\), отсюда \(x = \sqrt(3){a \cdot b \cdot c}\)
3) \(x = \sqrt(3){8 \cdot 12 \cdot 18} = \sqrt(3){12 \cdot (8 \cdot 18)} = \sqrt(3){12 \cdot 144} = \sqrt{12^2 \cdot 12} = 12 \text{ см}\)

Ответ: Ребро куба равно 12 см.

Дано:
Размеры прямоугольного параллелепипеда: a = 8 см, b = 12 см, c = 18 см.
Требуется найти ребро куба, объём которого равен объёму данного параллелепипеда.

Решение:

1) Объём параллелепипеда вычисляется по формуле:
\(V_{парал} = a \cdot b \cdot c = 8 \cdot 12 \cdot 18 = 1728 \text{ см}^3\)

2) Объём куба вычисляется по формуле:
\(V_{куба} = x^3\)
где x — ребро куба.

3) Так как объёмы параллелепипеда и куба равны, то:
\(1728 = x^3\)

4) Извлекая кубический корень, получаем:
\(x = \sqrt(3){1728} = 12 \text{ см}\)

Ответ: Ребро куба равно 12 см.