
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1193 Атанасян — Подробные Ответы
Дано: прямоугольный параллелепипед с измерениями:
а) 1, 1, 2
б) 8, 9, 12
в) √39, 7, 9
Вот извлечённое решение с правильным оформлением формул:
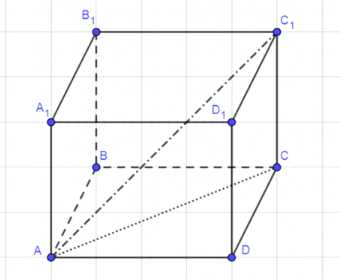
Дано: ABCDA₁B₁C₁D₁ — параллелепипед;
a) AB = BC = 1; CC₁ = 2;
б) AB = 8; BC = 9; CC₁ = 12;
в) AB = √39; BC = 7; CC₁ = 9;
Найти: AC₁ — ?
Решение:
a)
1) По теореме Пифагора:
\(AC = \sqrt{AB^2 + BC^2} = \sqrt{1^2 + 1^2} = \sqrt{2}\)
2) \(AC_1 = \sqrt{AC^2 + (CC_1)^2} = \sqrt{2 + 2^2} = \sqrt{6}\)
б)
1) По теореме Пифагора:
\(AC = \sqrt{AB^2 + BC^2} = \sqrt{8^2 + 9^2} = \sqrt{145}\)
2) \(AC_1 = \sqrt{AC^2 + (CC_1)^2} = \sqrt{145 + 12^2} = \sqrt{289} = 17\)
в)
1) По теореме Пифагора:
\(AC = \sqrt{AB^2 + BC^2} = \sqrt{39 + 7^2} = \sqrt{88}\)
2) \(AC_1 = \sqrt{AC^2 + (CC_1)^2} = \sqrt{88 + 81} = \sqrt{169} = 13\)
Ответ:
а) \(\sqrt{6}\)
б) \(17\)
в) \(13\)
Дано: прямоугольный параллелепипед ABCDA₁B₁C₁D₁. Требуется найти длину пространственной диагонали AC₁ для трёх различных наборов исходных данных. Рассмотрим каждый случай с полной детализацией всех шагов решения.
Случай а) Исходные данные: AB = 1, BC = 1, CC₁ = 2.
1. Найдём длину диагонали AC основания ABCD по теореме Пифагора для прямоугольного треугольника ABC:
\(AC = \sqrt{AB^2 + BC^2} = \sqrt{1^2 + 1^2} = \sqrt{1 + 1} = \sqrt{2}\)
2. Теперь найдём длину пространственной диагонали AC₁, рассматривая прямоугольный треугольник ACC₁:
\(AC₁ = \sqrt{AC^2 + CC₁^2} = \sqrt{(\sqrt{2})^2 + 2^2} = \sqrt{2 + 4} = \sqrt{6}\)
Ответ для случая а): \(\sqrt{6}\)
Случай б) Исходные данные: AB = 8, BC = 9, CC₁ = 12.
1. Вычисляем диагональ основания AC:
\(AC = \sqrt{AB^2 + BC^2} = \sqrt{8^2 + 9^2} = \sqrt{64 + 81} = \sqrt{145}\)
2. Находим пространственную диагональ AC₁:
\(AC₁ = \sqrt{AC^2 + CC₁^2} = \sqrt{145 + 12^2} = \sqrt{145 + 144} = \sqrt{289} = 17\)
Ответ для случая б): \(17\)
Случай в) Исходные данные: AB = √39, BC = 7, CC₁ = 9.
1. Вычисляем диагональ основания AC:
\(AC = \sqrt{AB^2 + BC^2} = \sqrt{(\sqrt{39})^2 + 7^2} = \sqrt{39 + 49} = \sqrt{88}\)
2. Находим пространственную диагональ AC₁:
\(AC₁ = \sqrt{AC^2 + CC₁^2} = \sqrt{88 + 9^2} = \sqrt{88 + 81} = \sqrt{169} = 13\)
Ответ для случая в): \(13\)
Во всех случаях решение основано на последовательном двукратном применении теоремы Пифагора: сначала для нахождения диагонали основания, затем для нахождения пространственной диагонали параллелепипеда.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!