ГДЗ по Геометрии 9 класс Номер 1189 Атанасян — Подробные Ответы

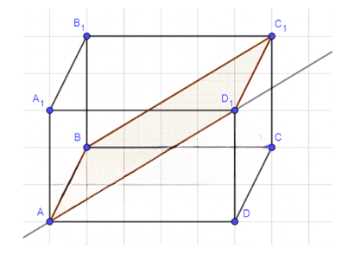
Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью1: а) ABС1; б) ACС1. Докажите, что построенные сечения — параллелограммы.

Доказательство:
1) Противоположные стороны сечения — противоположные ребра параллелепипеда, значит они равны и параллельны;
2) Вторая пара сторон — диагонали противоположных граней параллелепипеда, значит они также равны и параллельны;
3) Следовательно, сечения — параллелограммы.

Построение:
a)

1) Соединим точки BC₁;
2) Грани BB₁CC₁ и AA₁DD₁ параллельны, проведём прямую через A, параллельную BC₁;
3) Точка пересечения — D₁.

б)

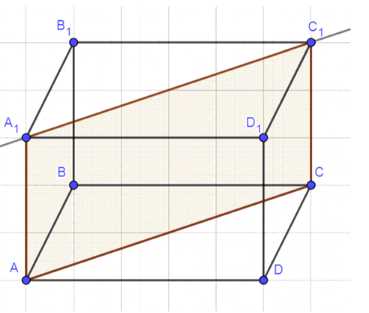
1) Соединим точки AC;
2) Грани ABCD и A₁B₁C₁D₁ параллельны, проведём прямую через C₁, параллельную AC;
3) Точка пересечения — A₁.

Доказательство:
1) Противоположные стороны построенного сечения являются противоположными ребрами параллелепипеда, значит они равны и параллельны;
2) Вторая пара сторон является диагоналями противоположных граней параллелепипеда, значит они также равны и параллельны;
3) Следовательно построенные сечения являются параллелограммами, что и требовалось доказать.

Построение:
a)
1) Соединим токи BC1;
2) Грани BB1CC1 и AA1DD1 — параллельны, поэтому в построим прямую через точку А строим прямую параллельную BC1;
3) В точке пересечения этой прямой и ребра отметим точку, данная точка уже есть — это точка D1;

б)
1) Соединим токи АС;
2) Грани ABCD и A1B1C1D1 — параллельны, поэтому в построим прямую через точку С1 строим прямую параллельную АС;
3) В точке пересечения этой прямой и ребра отметим точка уже есть — это точка А1;