Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
Почему этот учебник так ценят:
1. Удобная структура.
Все темы разбиты на логичные и последовательные разделы. Это позволяет легко находить нужный материал и шаг за шагом разбираться в геометрии.
2. Понятный язык.
Объяснения написаны так, чтобы даже сложные вещи стали простыми. Автор старается говорить с учениками на доступном и понятном языке.
3. Задачи для всех.
В учебнике есть задания как для новичков, так и для тех, кто хочет углубиться в тему. Это помогает каждому ученику найти что-то по силам и прокачать свои знания.
4. Наглядность.
Рисунки и схемы делают материал более понятным. Они помогают представить фигуры, их свойства и взаимосвязи.
5. Примеры из жизни.
Многие задачи связаны с реальными ситуациями, что делает геометрию ближе к повседневной жизни. Это не просто теория, а то, что можно применить на практике.
6. Помощь для учителей.
Учебник включает советы и рекомендации, которые помогают преподавателям проводить интересные и продуктивные уроки.
Итог:
Учебник Атанасяна — это не просто книга, а настоящий проводник в мир геометрии. Он помогает не только понять предмет, но и полюбить его. С ним учеба становится проще, интереснее и полезнее.
ГДЗ по Геометрии 9 класс Номер 1188 Атанасян — Подробные Ответы
На трёх рёбрах параллелепипеда даны точки А, В и С. Постройте сечение параллелепипеда плоскостью, проходящей через эти точки.
Решение
При построении сечений параллелепипеда нужно руководствоваться следующим правилом (оно будет обосновано в курсе стереометрии в 10 классе): отрезки, по которым секущая плоскость пересекает две противоположные грани параллелепипеда, параллельны.
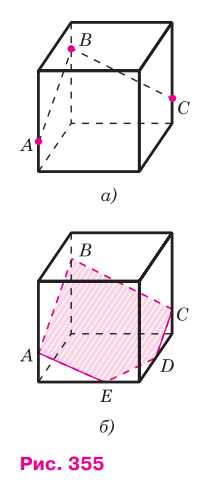
1) Рассмотрим сначала случай расположения точек А, В и С, изображённый на рисунке 355, а. Проведём отрезки АВ и ВС.
Далее, руководствуясь указанным правилом, через точку А проведём в плоскости передней грани прямую, параллельную ВС, а через точку С в плоскости боковой грани проведём прямую, параллельную АВ. Пересечения этих прямых с рёбрами нижней грани дают точки Е и D (рис. 355, б). Остаётся провести отрезок DE, и искомое сечение — пятиугольник ABCDE — построено.
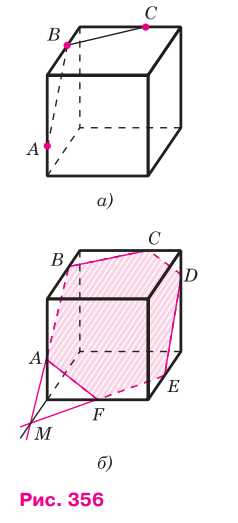
2) Обратимся теперь к случаю, представленному на рисунке 356, а. Этот случай более трудный, чем предыдущий. Можно провести отрезки АВ и ВС (см. рис. 356, а), но что делать дальше? Поступим так. Сначала построим прямую, по которой секущая плоскость пересекается с плоскостью нижнего основания параллелепипеда. С этой целью продолжим отрезок АВ и нижнее ребро, лежащее в той же грани, что и отрезок АВ, до пересечения в точке М (рис. 356, б). Далее, через точку М проведём в плоскости нижнего основания прямую, параллельную ВС. Это и есть та прямая, по которой секущая плоскость пересекается с плоскостью нижнего основания. Эта прямая пересекается с рёбрами нижнего основания в точках Е и F. Затем через точку Е проведём прямую, параллельную прямой АВ, и получим точку D. Наконец, проведём отрезки AF и CD, и искомое сечение — шестиугольник ABCDEF — построено.
Решение:
1) Рассмотрим случай, когда точки А, В и С расположены, как показано на рисунке 355, а. Проведем отрезки АВ и ВС.
2) Согласно правилу, отрезки, по которым секущая плоскость пересекает две противоположные грани параллелепипеда, параллельны. Поэтому через точку А проведем прямую, параллельную ВС, а через точку С — прямую, параллельную АВ. Пересечения этих прямых с ребрами нижней грани дают точки Е и D.
3) Соединив точки ABCDE, получаем искомое сечение — пятиугольник.
Второй случай представлен на рисунке 356, а.
1) Сначала продолжим отрезок АВ и ребро, лежащее в той же грани, до пересечения в точке М.
2) Через точку М проведем в плоскости нижнего основания прямую, параллельную ВС. Эта прямая пересекает ребра нижней грани в точках Е и F.
3) Через точку Е проведем прямую, параллельную АВ, и получим точку D.
4) Соединив точки ABCDEF, получаем искомое сечение — шестиугольник.
Таким образом, в зависимости от расположения точек А, В и С, сечение параллелепипеда может быть пятиугольником или шестиугольником.
Решение:
При построении сечений параллелепипеда необходимо руководствоваться следующим правилом: отрезки, по которым секущая плоскость пересекает две противоположные грани параллелепипеда, параллельны.
Рассмотрим два случая расположения точек А, В и С на рёбрах параллелепипеда.
Случай 1 (рис. 355, а):
1) Проведём отрезки АВ и ВС.
2) Согласно правилу, через точку А проведём в плоскости передней грани прямую, параллельную ВС, а через точку С в плоскости боковой грани проведём прямую, параллельную АВ.
3) Пересечения этих прямых с рёбрами нижней грани дают точки Е и D (рис. 355, б).
4) Соединив точки ABCDE, получаем искомое сечение — пятиугольник.
Случай 2 (рис. 356, а):
1) Проведём отрезки АВ и ВС.
2) Сначала построим прямую, по которой секущая плоскость пересекается с плоскостью нижнего основания параллелепипеда. Для этого продолжим отрезок АВ и нижнее ребро, лежащее в той же грани, до пересечения в точке М (рис. 356, б).
3) Через точку М проведём в плоскости нижнего основания прямую, параллельную ВС. Эта прямая пересекает ребра нижней грани в точках Е и F.
4) Через точку Е проведём прямую, параллельную АВ, и получим точку D.
5) Соединив точки ABCDEF, получаем искомое сечение — шестиугольник.
Таким образом, в зависимости от расположения точек А, В и С, сечение параллелепипеда может быть пятиугольником или шестиугольником.
Геометрия
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.