Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
Почему этот учебник так ценят:
1. Удобная структура.
Все темы разбиты на логичные и последовательные разделы. Это позволяет легко находить нужный материал и шаг за шагом разбираться в геометрии.
2. Понятный язык.
Объяснения написаны так, чтобы даже сложные вещи стали простыми. Автор старается говорить с учениками на доступном и понятном языке.
3. Задачи для всех.
В учебнике есть задания как для новичков, так и для тех, кто хочет углубиться в тему. Это помогает каждому ученику найти что-то по силам и прокачать свои знания.
4. Наглядность.
Рисунки и схемы делают материал более понятным. Они помогают представить фигуры, их свойства и взаимосвязи.
5. Примеры из жизни.
Многие задачи связаны с реальными ситуациями, что делает геометрию ближе к повседневной жизни. Это не просто теория, а то, что можно применить на практике.
6. Помощь для учителей.
Учебник включает советы и рекомендации, которые помогают преподавателям проводить интересные и продуктивные уроки.
Итог:
Учебник Атанасяна — это не просто книга, а настоящий проводник в мир геометрии. Он помогает не только понять предмет, но и полюбить его. С ним учеба становится проще, интереснее и полезнее.
ГДЗ по Геометрии 9 класс Номер 1183 Атанасян — Подробные Ответы
Даны параллельные прямые b и с и точка А, не лежащая ни на одной из них. Постройте равносторонний треугольник АВС так, чтобы вершины В и С лежали соответственно на прямых b и с. Сколько решений имеет задача?
Решение
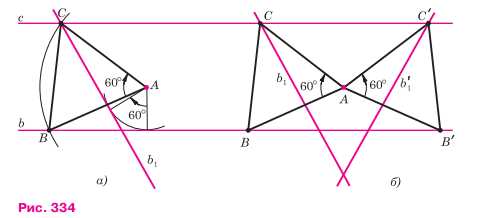
Допустим, что задача решена и искомый треугольник АВС по- строен (рис. 334, а). При повороте плоскости вокруг точки А на 60° по часовой стрелке вершина В отображается в вершину С, поэтому прямая b отображается на прямую b1, проходящую через точку С. Прямую b, легко построить, не пользуясь точками В и С (см. задачу 1171). Построив прямую b1, находим точку С, в которой прямая b, пересекается с прямой с. Затем, построив окружность с центром А радиуса АС, находим точку В. На рисунке 334, а выполнено построение.
Задача имеет два решения, одно из которых получается при повороте плоскости вокруг точки А на 60° по часовой стрелке (ДАВС на рисунке 334, а), а другое — при повороте плоскости на угол 60° против часовой стрелки (ДАВ’С’ на рисунке 334, б).
Решение:
Даны параллельные прямые b и c и точка A, не лежащая ни на одной из них. Необходимо построить равносторонний треугольник ABC, где вершины B и C лежат соответственно на прямых b и c.
Пусть задача решена и треугольник ABC построен (рис. 334, а). При повороте плоскости вокруг точки A на 60° по часовой стрелке вершина B отображается в вершину C, поэтому прямая b отображается на прямую b₁, проходящую через точку C. Прямую b можно построить, не используя точки B и C (см. задачу 1171). Построив прямую b₁, находим точку C, в которой прямая b пересекается с прямой c. Затем, построив окружность с центром A и радиусом AC, находим точку B.
Задача имеет два решения: одно при повороте плоскости вокруг точки A на 60° по часовой стрелке (ΔABC на рис. 334, а), другое — при повороте на 60° против часовой стрелки (ΔABC’ на рис. 334, б).
Решение:
Дано: параллельные прямые b и c, а также точка A, не лежащая ни на одной из этих прямых. Требуется построить равносторонний треугольник ABC, где вершины B и C лежат соответственно на прямых b и c.
Предположим, что задача решена и искомый треугольник ABC построен (рис. 334, а). При повороте плоскости вокруг точки A на 60° по часовой стрелке вершина B отображается в вершину C, поэтому прямая b отображается на прямую b₁, проходящую через точку C.
Для построения прямой b₁ не требуется использовать точки B и C (см. задачу 1171). Построив прямую b₁, находим точку C, в которой прямая b пересекается с прямой c. Затем, построив окружность с центром в точке A и радиусом AC, находим точку B.
Таким образом, построение треугольника ABC выполняется следующим образом:
1. Построить прямую b₁, проходящую через точку C и параллельную прямой b.
2. Найти точку C, в которой прямая b пересекается с прямой c.
3. Построить окружность с центром в точке A и радиусом AC. Точка пересечения этой окружности с прямой b₁ будет являться вершиной B.
Задача имеет два решения:
1. Первое решение получается при повороте плоскости вокруг точки A на 60° по часовой стрелке (треугольник ABC на рис. 334, а).
2. Второе решение получается при повороте плоскости вокруг точки A на 60° против часовой стрелки (треугольник AB’C’ на рис. 334, б).
Таким образом, данная задача имеет два возможных решения.
Геометрия
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.