
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1180 Атанасян — Подробные Ответы
В окружность с центром О вписаны два равносторонних треугольника ABC и A1B1C1, причём вершины обозначены так,
что направление обхода по дуге ABC от точки А к точке С совпадает с направлением обхода по дуге А1В1С1 от точки А1
к точке С1. Используя поворот вокруг точки О, докажите, что прямые AA1, BB1 и СС1 либо проходят через точку О, либо,
пересекаясь, образуют равносторонний треугольник.
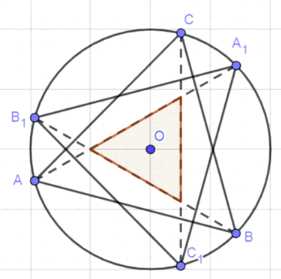
Дано: В окружность с центром O вписаны два равносторонних треугольника ABC и A1B1C1, причем направление обхода по дуге ABC от точки A к точке C совпадает с направлением обхода по дуге A1B1C1 от точки A1 к точке C1.
Доказать: Прямые AA1, BB1 и CC1 либо проходят через точку O, либо, пересекаясь, образуют равносторонний треугольник.
Доказательство:
1) Рассмотрим поворот вокруг точки O на 120°, при котором вершина A отображается на вершину B. При этом вершина B отображается на вершину C, а вершина C — на вершину A. Вершина A1 отображается на вершину B1, а значит, прямая AA1 отображается на BB1. Аналогично прямая BB1 отображается на CC1, а CC1 на AA1.
2) Если прямая AA1 проходит через центр O, то и BB1, CC1 также проходят через точку O. Если же прямая AA1 не проходит через точку O, то и BB1 не проходит через точку O, и прямые AA1 и BB1 при пересечении образуют угол в 60°. Аналогично и для прямых BB1 и CC1.
3) Таким образом, прямые AA1, BB1 и CC1 либо проходят через точку O, либо, пересекаясь, образуют равносторонний треугольник.
Дано: В окружность с центром O вписаны два равносторонних треугольника ABC и A1B1C1, причем направление обхода по дуге ABC от точки A к точке C совпадает с направлением обхода по дуге A1B1C1 от точки A1 к точке C1.
Доказать: Прямые AA1, BB1 и CC1 либо проходят через точку O, либо, пересекаясь, образуют равносторонний треугольник.
Доказательство:
1) Рассмотрим поворот вокруг точки O на 120°, при котором вершина A отображается на вершину B. При этом вершина B отображается на вершину C, а вершина C — на вершину A.
2) Кроме того, вершина A1 отображается на вершину B1, а значит, прямая AA1 отображается на BB1. Аналогично прямая BB1 отображается на CC1, а CC1 на AA1.
3) Если прямая AA1 проходит через центр O, то и BB1, CC1 также проходят через точку O (рисунок а).
4) Если же прямая AA1 не проходит через точку O, то и BB1 не проходит через точку O. В таком случае прямые AA1 и BB1 при пересечении образуют угол в 60°. Аналогично и для прямых BB1 и CC1.
5) Значит, прямые AA1, BB1 и CC1 при пересечении образуют равносторонний треугольник.
Если прямая AA1 проходит через центр O, то и BB1, CC1 также проходят через точку O.
Если прямая AA1 не проходит через точку O, то и BB1 не проходит через точку O, и прямые AA1 и BB1 при пересечении образуют угол в 60°.
Таким образом, доказано, что прямые AA1, BB1 и CC1 либо проходят через точку O, либо, пересекаясь, образуют равносторонний треугольник.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!