Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1179 Атанасян — Подробные Ответы
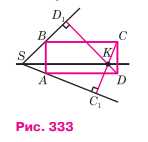
На стороне AB прямоугольника ABCD построен треугольник ABS так, как показано на рисунке 333: CC1 ⊥ AS, DD1 ⊥ BS. Используя параллельный перенос, докажите, что прямые SK и AB взаимно перпендикулярны.
Дано: ABCD — прямоугольник; ΔABS; CC1 ⊥ AS; DD1 ⊥ BS;
Доказать: SK ⊥ AB;
Доказательство:
1) Осуществим параллельный перенос ABSA на ВС, его образом будет ACS1D;
2) SB ∥ S1C и SA ∥ S1D так как по условию: DD1 ⊥ SB и CC1 ⊥ SA, значит D1 ∥ S1C, следовательно К — точка пересечения высот ACS1D и S1K ⊥ CD, отсюда SK ⊥ AB, что и требовалось доказать.
Дано: ABCD — прямоугольник; ΔABS; CC1 ⊥ AS; DD1 ⊥ BS;
Доказать: SK ⊥ AB;
Доказательство:
1) Осуществим параллельный перенос треугольника ΔABS на сторону ВС прямоугольника ABCD. Образом треугольника ΔABS будет треугольник ΔAC₁S₁D.
2) Так как по условию DD₁ ⊥ SB и CC₁ ⊥ AS, то D₁ || S₁C. Следовательно, точка K является точкой пересечения высот треугольника ΔAC₁S₁D.
3) Поскольку S₁K ⊥ CD, то SK ⊥ AB, что и требовалось доказать.
Таким образом, используя параллельный перенос треугольника ΔABS на сторону ВС прямоугольника ABCD, мы доказали, что прямые SK и AB взаимно перпендикулярны.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.