Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1178 Атанасян — Подробные Ответы
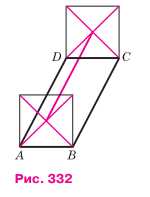
На сторонах AB и CD параллелограмма ABCD построены квадраты так, как показано на рисунке 332. Используя параллельный перенос, докажите, что отрезок, соединяющий центры этих квадратов, равен и параллелен стороне AD.
Дано: ABCD — параллелограмм; AA₁B₁B; DD₁C₁C — квадраты; O и O₁ — центры квадратов.
Доказательство:
1) AD = BC, так как ABCD — параллелограмм и AB = DC.
2) O и O₁ — середины A₁B и D₁C, значит OO₁ = BC = AD.
3) OO₁ || AD, так как AOO₁ — параллелограмм.
Таким образом, отрезок, соединяющий центры квадратов, равен и параллелен стороне AD параллелограмма ABCD.
Дано: ABCD — параллелограмм; AA₁B₁B; DD₁C₁C — квадраты; O и O₁ — центры квадратов.
Доказательство:
1) Рассмотрим параллельный перенос на вектор AD: AD = BC, так как ABCD — параллелограмм (по условию) и AA₁B₁B и DD₁C₁C — квадраты, AB = DC (по свойству параллелограмма), значит AA₁B₁B = DD₁C₁C.
2) AA₁ = DD₁ и AA₁ || DD₁, следовательно AA₁D₁D — параллелограмм.
3) A₁D₁ = AD = BC, следовательно A₁D₁CB — параллелограмм.
4) O и O₁ — середины A₁B и D₁C (по условию), значит A₁B = D₁C, следовательно OO₁ = BC = AD, значит AOO₁ — параллелограмм, отсюда OO₁ = AD и OO₁ || AD.
Таким образом, доказано, что отрезок, соединяющий центры квадратов, равен и параллелен стороне AD параллелограмма ABCD.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.