ГДЗ по Геометрии 9 класс Номер 1177 Атанасян — Подробные Ответы

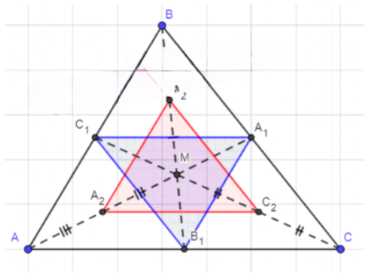
Дано: Медианы AA1, BB1 и CC1 треугольника ABC пересекаются в точке M. Точки A2, B2 и C2 являются соответственно серединами отрезков AM, BM и CM.

Доказать: ΔA1B1C1 = ΔA2B2C2

Решение:
1) Так как M — точка пересечения медиан треугольника ABC, то AM = 2MA1. Отсюда, учитывая, что точка A2 — середина отрезка AM, получаем MA1 = MA2, т.е. точки A1 и A2 симметричны относительно точки M.
2) Аналогично точки B1 и B2, а также точки C1 и C2 симметричны относительно точки M.
3) Рассмотрим центральную симметрию относительно точки M. При этой симметрии точки A1, B1, C1 отображаются в точки A2, B2, C2, поэтому треугольник ΔA1B1C1 отображается на треугольник ΔA2B2C2, и, следовательно, ΔA1B1C1 = ΔA2B2C2.

Дано: ΔABC; AA1 ∩ BB1 ∩ CC1 = M; A2, B2, C2 — середины АМ, ВМ, СМ;

Доказать: ΔA1B1C1 = ΔA2B2C2;

Доказательство:

1) Так как M — точка пересечения медиан ΔABC, то AM = 2MA1, отсюда MA1 = MA2 (так как A2 — середина отрезка AM), то есть A1 и A2 симметричны относительно точки M;
2) То же справедливо и для точек B1 и B2; C1 и C2;
3) Рассмотрим центральную симметрию относительно точки M: Точки A1, B1 и C1 отображаются в точки A2, B2 и C2. Следовательно, ΔA1B1C1 отображается в ΔA2B2C2. Значит, ΔA1B1C1 = ΔA2B2C2, что и требовалось доказать.

Дано: Медианы AA1, BB1 и CC1 треугольника ABC пересекаются в точке M. Точки A2, B2 и C2 являются соответственно серединами отрезков AM, BM и CM.

Доказать: ΔA1B1C1 = ΔA2B2C2

Решение:

1) Так как M — точка пересечения медиан треугольника ABC, то AM = 2MA1. Отсюда, учитывая, что точка A2 — середина отрезка AM, получаем MA1 = 1/2 AM.
2) Аналогично, MB1 = 1/2 BM и MC1 = 1/2 CM.
3) Рассмотрим центральную симметрию относительно точки M. При этой симметрии:
— Точка A1 переходит в точку A2
— Точка B1 переходит в точку B2
— Точка C1 переходит в точку C2
4) Таким образом, треугольник ΔA1B1C1 симметричен треугольнику ΔA2B2C2 относительно точки M.
5) Следовательно, ΔA1B1C1 = ΔA2B2C2.

Вывод: Доказано, что ΔA1B1C1 = ΔA2B2C2.