ГДЗ по Геометрии 9 класс Номер 1176 Атанасян — Подробные Ответы

Даны острый угол ABC и точка D внутри него. Используя осевую симметрию, найдите на сторонах данного угла такие
точки Е и F, чтобы треугольник DEF имел наименьший периметр.

Дано: ΔABC — острый; D — лежит внутри ΔABC; E ∈ BA; F ∈ BC;
Найти: E и F так, чтобы периметр ΔDEF был наименьшим;

Решение:

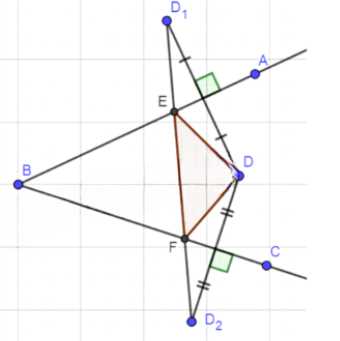
1) Построим точку D₁, симметричную точке D относительно луча BA, и точку D₂, симметричную точке D относительно луча BC;
2) D₁D₂ ∩ BA = E; D₁D₂ ∩ BC = F; ΔDEF — искомый;
3) Докажем, что это так:
По неравенству треугольника D₁D₂ < D₁D + DD₂, но D₁D₂ = DE + EF + FD₂;
D₁E = ED и FD₂ = FD, значит D₁D₂ = ED + EF + FD или D₁D = PDEF — он наименьший, так как DE + EF — наименьшая и DF + FE — наименьшая.

Дано: ΔABC — острый; D — лежит внутри ΔABC; E ∈ BA; F ∈ BC;
Найти: E и F так, чтобы периметр ΔDEF был наименьшим;

Решение:

1) Построим точку D₁, симметричную точке D относительно луча BA, и точку D₂, симметричную точке D относительно луча BC.

2) Докажем, что точки E и F, являющиеся пересечениями отрезка D₁D₂ с сторонами AB и AC соответственно, обеспечивают наименьший периметр треугольника DEF.

По неравенству треугольника:
D₁D₂ < D₁D + DD₂

Но D₁D₂ = DE + EF + FD₂
D₁E = ED
FD₂ = FD

Следовательно, D₁D₂ = ED + EF + FD или D₁D = P(DEF)

Так как DE + EF — наименьшая сумма расстояний от точки D до сторон AB и AC, а DF + FE — наименьшая сумма расстояний от точки D до сторон AC и AB, то периметр треугольника DEF будет наименьшим.

Таким образом, точки E и F, являющиеся пересечениями отрезка D₁D₂ со сторонами AB и AC соответственно, обеспечивают наименьший периметр треугольника DEF.