Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
Почему этот учебник так ценят:
1. Удобная структура.
Все темы разбиты на логичные и последовательные разделы. Это позволяет легко находить нужный материал и шаг за шагом разбираться в геометрии.
2. Понятный язык.
Объяснения написаны так, чтобы даже сложные вещи стали простыми. Автор старается говорить с учениками на доступном и понятном языке.
3. Задачи для всех.
В учебнике есть задания как для новичков, так и для тех, кто хочет углубиться в тему. Это помогает каждому ученику найти что-то по силам и прокачать свои знания.
4. Наглядность.
Рисунки и схемы делают материал более понятным. Они помогают представить фигуры, их свойства и взаимосвязи.
5. Примеры из жизни.
Многие задачи связаны с реальными ситуациями, что делает геометрию ближе к повседневной жизни. Это не просто теория, а то, что можно применить на практике.
6. Помощь для учителей.
Учебник включает советы и рекомендации, которые помогают преподавателям проводить интересные и продуктивные уроки.
Итог:
Учебник Атанасяна — это не просто книга, а настоящий проводник в мир геометрии. Он помогает не только понять предмет, но и полюбить его. С ним учеба становится проще, интереснее и полезнее.
ГДЗ по Геометрии 9 класс Номер 1175 Атанасян — Подробные Ответы
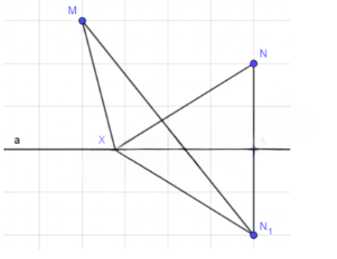
Даны прямая a и точки M и N, лежащие по одну сторону от неё. Докажите, что на прямой а существует единственная
точка X, такая, что сумма расстояний MX + XN имеет наименьшее значение.
Дано: а, М и N лежат по одну сторону от прямой а;
Доказать: существует единственная точка Х Є а такая, что MX + XN — имеет наименьшее значение;
Доказательство:
1) Пусть N1 симметрична И относительно прямой а. Так как отрезки XN и XN1 симметричны относительно прямой a, XN = XN1. Тогда MX + XN = MX + XN1;
2) Если точка Х не лежит на прямой MN1, то MX + XN1 > MN1, а если точка Х лежит на прямой MN1 (а значит и на отрезке MN1), то
MX + XN= MN1. Следовательно, сумма MX + XN1, а значит и равная ей MX + XN принимают наименьшее значение, только если точка Х является точкой пересечения а и MN1, что и требовалось доказать.
Дано: прямая а и точки М и N, лежащие по одну сторону от нее.
Доказательство:
1) Пусть N₁ — точка, симметричная N относительно прямой а. Тогда отрезки XN и XN₁ симметричны относительно прямой а, следовательно, XN = XN₁.
Таким образом, MX + XN = MX + XN₁.
2) Если точка X не лежит на прямой MN₁, то MX + XN₁ > MN₁. Если же точка X лежит на прямой MN₁ (а значит, и на отрезке MN₁), то MX + XN = MN₁.
Следовательно, сумма MX + XN₁, а значит, и равная ей сумма MX + XN, принимают наименьшее значение, только если точка X является точкой пересечения прямой а и прямой MN₁.
Таким образом, доказано, что на прямой а существует единственная точка X, такая, что сумма расстояний MX + XN имеет наименьшее значение. Эта точка X является точкой пересечения прямой а и прямой MN₁.
Геометрия
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.