
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1174 Атанасян — Подробные Ответы
Докажите, что два прямоугольника равны, если: а) смежные стороны одного прямоугольника соответственно равны смежным сторонам другого; б) сторона и диагональ одного прямоугольника соответственно равны стороне и диагонали другого.
Дано:
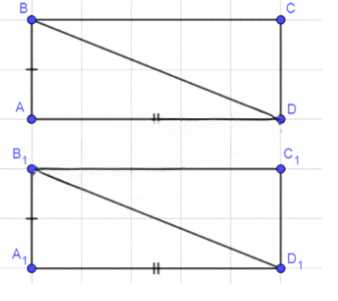
ABCD, A1B1C1D1 — прямоугольники;
a) AB = A1B1; AD = A1D1;
b) AB = A1B1; BD = B1D1;
Доказать:
ABCD = A1B1C1D1
Доказательство:
a)
1) ABCD и A1B1C1D1 — прямоугольники, значит: AB = CD = A1B1 = C1D1 и AD = BC = A1D1 = B1C1 (по свойству прямоугольника);
2) Отсюда ABCD = A1B1C1D1 (по признаку), что и требовалось доказать.
b)
1) ABCD и A1B1C1D1 — прямоугольники, значит: AB = CD = A1B1 = C1D1 и BC = AD, B1C = A1D1 (по свойству прямоугольника);
2) Рассмотрим ΔABD и ΔA1B1D1 — прямоугольные: AB = A1B1 и BD = B1D1, следовательно ΔABD = ΔA1B1D1 (по катету и гипотенузе);
3) Рассмотрим ABCD и AB1C1D1 — прямоугольные: DC = D1C1 и BD = B1D1, следовательно ABCD = AB1C1D1 (по катету и гипотенузе);
4) Получаем, что ABCD = A1B1C1D1 (по признаку), что и требовалось доказать.
Дано:
ABCD и A1B1C1D1 — прямоугольники.
Доказать:
a) Если смежные стороны одного прямоугольника соответственно равны смежным сторонам другого прямоугольника, то эти прямоугольники равны.
b) Если сторона и диагональ одного прямоугольника соответственно равны стороне и диагонали другого прямоугольника, то эти прямоугольники равны.
Доказательство:
a) Пусть AB = A1B1 и AD = A1D1.
1) Так как ABCD и A1B1C1D1 — прямоугольники, то AB = CD = A1B1 = C1D1 и AD = BC = A1D1 = B1C1 (по свойству прямоугольника).
2) Следовательно, ABCD = A1B1C1D1 (по признаку равенства прямоугольников).
b) Пусть AB = A1B1 и BD = B1D1.
1) Так как ABCD и A1B1C1D1 — прямоугольники, то AB = CD = A1B1 = C1D1 и BC = AD, B1C = A1D1 (по свойству прямоугольника).
2) Рассмотрим ΔABD и ΔA1B1D1. Так как AB = A1B1 и BD = B1D1, то ΔABD = ΔA1B1D1 (по признаку равенства прямоугольных треугольников).
3) Рассмотрим ABCD и AB1C1D1. Так как DC = D1C1 и BD = B1D1, то ABCD = AB1C1D1 (по признаку равенства прямоугольников).
4) Следовательно, ABCD = A1B1C1D1 (по переходу от равных фигур).
Таким образом, доказано, что если смежные стороны одного прямоугольника соответственно равны смежным сторонам другого прямоугольника, или если сторона и диагональ одного прямоугольника соответственно равны стороне и диагонали другого прямоугольника, то эти прямоугольники равны.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!