
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1171 Атанасян — Подробные Ответы
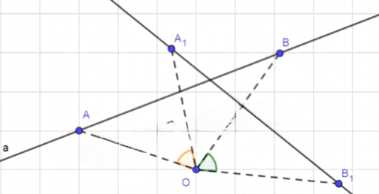
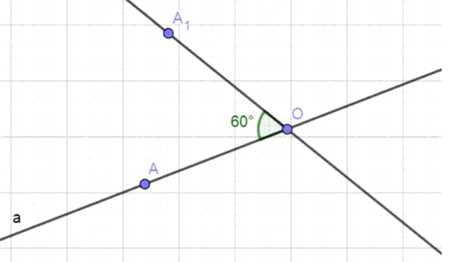
Постройте прямую а1, которая получается из данной прямой а поворотом вокруг точки О на угол 60° по часовой стрелке, если прямая а: а) не проходит через точку О; б) проходит через точку О.
Решение
а) Построим окружность с центром О, которая касается прямой а (объясните, как это сделать). Пусть M — точка касания. При повороте вокруг точки О эта окружность отображается на себя, а касательная а отображается на некоторую касательную a1 (объясните почему). Для построения прямой а1 построим сначала точку М1, в которую отображается точка M при повороте вокруг точки О на угол 60° по часовой стрелке, а затем проведём касательную а1 к окружности в точке M1.
а) Построим окружность с центром O, которая касается прямой a. Пусть M — точка касания. При повороте вокруг точки O эта окружность отображается на себя, а касательная a отображается на некоторую касательную a₁. Для построения прямой a₁ построим сначала точку M₁, в которую отображается точка M при повороте вокруг точки O на угол 60° по часовой стрелке, а затем проведём касательную a₁ к окружности в точке M₁.
б) Если прямая a проходит через точку O, то при повороте вокруг этой точки на угол 60° по часовой стрелке, прямая a отобразится на прямую a₁, которая составляет с исходной прямой a угол 60°.
а) Построение прямой a₁, которая получается из данной прямой a поворотом вокруг точки O на угол 60° по часовой стрелке, если прямая a не проходит через точку O:
1. Построим окружность с центром в точке O, которая касается прямой a. Пусть точка M будет точкой касания окружности и прямой a.
2. При повороте вокруг точки O эта окружность отображается на себя, а касательная a отображается на некоторую касательную a₁.
3. Для построения прямой a₁ сначала построим точку M₁, в которую отображается точка M при повороте вокруг точки O на угол 60° по часовой стрелке.
4. Затем проведём касательную a₁ к окружности в точке M₁. Полученная прямая a₁ и будет искомой.
б) Построение прямой a₁, которая получается из данной прямой a поворотом вокруг точки O на угол 60° по часовой стрелке, если прямая a проходит через точку O:
1. Если прямая a проходит через точку O, то при повороте вокруг этой точки на угол 60° по часовой стрелке, прямая a отобразится на прямую a₁.
2. Прямая a₁ будет составлять с исходной прямой a угол 60°.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!