
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1169 Атанасян — Подробные Ответы
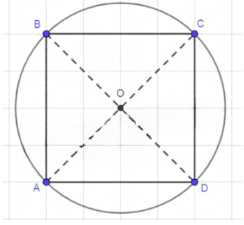
Докажите, что при повороте квадрата вокруг точки пересечения его диагоналей на угол 90° квадрат отображается на себя.
Доказательство:
1) O — центр описанной окружности O(O, R), так как O — точка пересечения диагоналей квадрата.
2) Все вершины лежат на описанной окружности и отображаются друг на друга при определенных углах поворота.
3) ABCD — квадрат, значит он делит описанную окружность на четыре равных дуги: \(360^\circ \div 4 = 90^\circ\).
4) При вращении на 90°, каждая вершина квадрата будет отражаться на соседнюю вершину, и ABCD отразится сам на себя.
Доказательство:
1) O — точка пересечения диагоналей квадрата, значит O — центр описанной окружности O(O, R);
2) Все вершины лежат на описанной окружности и отображаются друг на друга при определенных углах поворота;
3) Рассмотрим поворот на 90°: ABCD — квадрат, значит он делит описанную окружность на четыре равных дуги; \(360^\circ \div 4 = 90^\circ\);
4) Вращением называется движение точки по дуге окружности с центром в точке, вокруг которой производится вращение;
5) Центром вращения и центром описанной окружности является одна точка, следовательно при вращении на 90°, каждая вершина квадрата будет отражаться на соседнюю вершину и ABCD отразится сам на себя, что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!