Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1167 Атанасян — Подробные Ответы
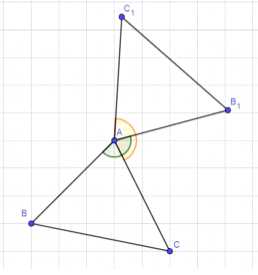
Постройте треугольник, который получается из данного треугольника ABC поворотом вокруг точки А на угол 150° против часовой стрелки.
Согласно изображению, необходимо построить фигуру AA1B1C1, которая получается из данной фигуры ABC путем вращения вокруг точки А на 150° против часовой стрелки. Построение выполняется следующим образом:
1. Установить транспортир так, чтобы значение 0° было со стороны точки А.
2. Построить углы в 75° со сторонами ВА и СА.
3. Отметить точки C1 и B1 на расстоянии AC и AB соответственно.
4. Соединить точки A, C1 и B1.
Подробное решение построения треугольника AA₁B₁C₁, полученного из треугольника ABC поворотом на 150° против часовой стрелки вокруг точки A:
1. Построим вспомогательный угол в 75° со стороной ВА. Для этого:
— Установим транспортир так, чтобы значение 0° было со стороны точки А.
— Отложим угол в 75° от стороны ВА.
2. Отметим точку C₁ на расстоянии AC от точки А.
3. Отметим точку B₁ на расстоянии AB от точки А.
4. Соединим точки A, C₁ и B₁, получив треугольник AA₁B₁C₁.
Таким образом, мы построили искомый треугольник AA₁B₁C₁, который получается из треугольника ABC поворотом на 150° против часовой стрелки вокруг точки A.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.