ГДЗ по Геометрии 9 класс Номер 1165 Атанасян — Подробные Ответы

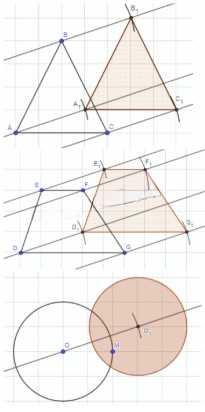
Даны треугольник, трапеция и окружность. Постройте фигуры, которые получаются из этих фигур параллельным переносом на данный вектор а.

Построение параллельного переноса фигур:

1) Для треугольника и трапеции:
Построим прямые, проходящие через вершины данных фигур и параллельные вектору a.
Для окружности: прямую через точку 0.

2) Для всех фигур:
Установим циркуль на длину вектора a и построим дуги, с центрами на вершинах этих фигур, проходящие через прямые на которых они лежат, отметим точки пересечения данных дуг и прямых со стороны, в которую направлен вектор.

3) Для треугольника и трапеции: соединим эти точки.

4) Для окружности: установим раствор циркуля на OM и построим окружность с центром в точке O1.

Решение:

Для построения фигур, полученных параллельным переносом данных треугольника, трапеции и окружности на вектор a, выполним следующие шаги:

1. Для треугольника и трапеции:
— Построим прямые, проходящие через вершины этих фигур и параллельные вектору a.
— Для окружности построим прямую, проходящую через точку O.

2. Для всех фигур:
— Установим циркуль на длину вектора a и построим дуги с центрами в вершинах фигур, проходящие через прямые, на которых лежат соответствующие вершины.
— Отметим точки пересечения этих дуг и прямых со стороны, в которую направлен вектор a.

3. Для треугольника и трапеции:
— Соединим отмеченные точки, получив новые фигуры, параллельно перенесенные на вектор a.

4. Для окружности:
— Установим раствор циркуля, равный длине отрезка OM, и построим окружность с центром в точке O1.

В результате выполнения этих действий мы получим фигуры, являющиеся параллельным переносом исходных треугольника, трапеции и окружности на вектор a.