
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1164 Атанасян — Подробные Ответы
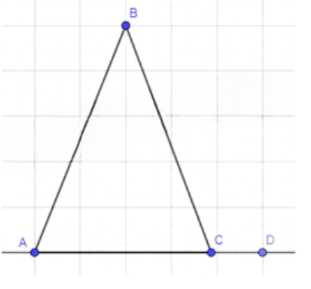
Даны равнобедренный треугольник ABC с основанием AC и такая точка D на прямой AC, что точка С лежит на отрезке
AD. а) Постройте отрезок В1D, который получается из отрезка ВС параллельным переносом на вектор CD. б) Докажите, что
четырёхугольник ABB1D — равнобедренная трапеция.
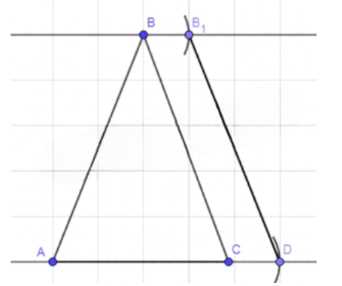
а) Построение:
1) Построим прямую, проходящую через точку В и параллельную АС.
2) Установим раствор циркуля на длину вектора CD и проведем дуги с центрами в точках В и С, проходящие через прямые, на которых они лежат.
3) Отметим точки В1 и D на пересечении дуг и прямых, соединим эти точки.
Таким образом, мы построили фигуру B1D, как было указано в условии.
б) Дано: ΔABC — равнобедренный; AB = BC;
Доказать: ABB1D — равнобедренная трапеция;
Доказательство:
1) При параллельном переносе, сохраняются длины отрезков, значит: BB1 = CD, BB1 ∥ CD и BC ∥ B1D, следовательно BB1CD — параллелограмм, отсюда B1D = BC.
2) В четырехугольнике ABB1D: BB1 ∥ AD (так как BB1 ∥ CD и C ∈ AD), AB ≅ B1D (так как B1D = BC и AB = BC), следовательно ABB1D — равнобедренная трапеция, что и требовалось доказать.
Для решения задачи, начнем с построения фигуры B1D и затем перейдем к доказательству, что четырехугольник ABB1D является равнобедренной трапецией.
1. Построение фигуры B1D:
— Проведем прямую, проходящую через точку B и параллельную отрезку AC. Эта прямая будет служить основой для дальнейших построений.
— Установим раствор циркуля на длину вектора CD и проведем дуги с центрами в точках B и C. Эти дуги пересекут прямые, на которых лежат точки B и C.
— Обозначим точки пересечения дуг с прямыми как B1 и D соответственно. Соединим точки B1 и D отрезком.
Таким образом, мы построили фигуру B1D, как указано в условии.
2. Доказательство, что четырехугольник ABB1D является равнобедренной трапецией:
— Из условия известно, что треугольник ΔABC является равнобедренным, то есть AB = BC.
— При параллельном переносе сохраняются длины отрезков, следовательно, BB1 = CD. Поскольку прямая BB1 параллельна CD, и BC также параллельна B1D, это означает, что BB1CD является параллелограммом. Из этого следует, что B1D = BC.
— Теперь рассмотрим четырехугольник ABB1D. Поскольку BB1 параллельно AD (так как BB1 параллельно CD и C принадлежит AD), и AB равно B1D (так как B1D = BC и AB = BC), мы можем заключить, что AB ≅ B1D.
— Таким образом, в четырехугольнике ABB1D две пары противоположных сторон равны и параллельны, что по определению равнобедренной трапеции подтверждает, что ABB1D является равнобедренной трапецией.
Таким образом, мы доказали, что четырехугольник ABB1D является равнобедренной трапецией, что и требовалось доказать.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!