ГДЗ по Геометрии 9 класс Номер 1163 Атанасян — Подробные Ответы

Начертите треугольник ABC, вектор ММ1ξ, который не параллелен ни одной из сторон треугольника, и вектор аα, параллельный стороне AC. Постройте треугольник A1B1C1, который получается из треугольника ABC параллельным переносом: а) на вектор ММ1ξ; б) на вектор aα

1) Построение а):
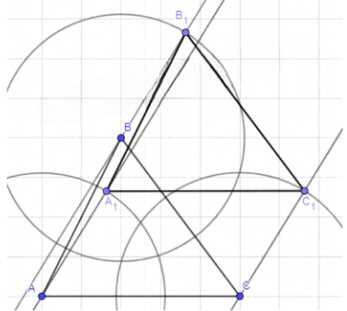
— Построим прямые, параллельные вектору ММ1 через точки А, В и С.
— Построим окружности с центрами в точках А, В и С и радиусом ММ1.
— На пересечении данных окружностей и прямых, лежащих на точках, через центр которых они проходят, отметим точки А1, В1 и С1 со стороны, в которую направлен вектор.
— Соединим точки А1, В1 и С1.

2) Построение б):
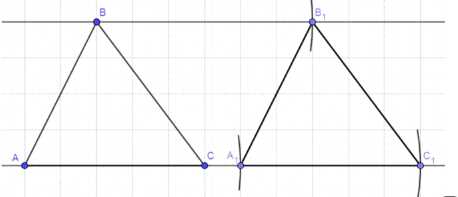
— Построим продолжение прямой АС, а также прямую, проходящую через точку В и параллельную АС.
— Установим раствор циркуля на длину вектора а и проведем дуги с центрами в точках А, В и С, проходящие через прямые, на которых они лежат.
— Отметим точки А1, В1 и С1 на пересечении дуг и прямых, соединим эти точки.

1) Построение а):

— Начнем с вектора \(\overrightarrow{MM_1}\). Обозначим его длину как \(d\).
— Построим прямые, параллельные вектору \(\overrightarrow{MM_1}\), через точки \(A\), \(B\) и \(C\). Эти прямые будут иметь одинаковый наклон, соответствующий направлению вектора.
— Далее, построим окружности с центрами в точках \(A\), \(B\) и \(C\) и радиусом \(d\). Уравнения окружностей можно записать как:
— Для точки \(A\): \((x — x_A)^2 + (y — y_A)^2 = d^2\)
— Для точки \(B\): \((x — x_B)^2 + (y — y_B)^2 = d^2\)
— Для точки \(C\): \((x — x_C)^2 + (y — y_C)^2 = d^2\)
— На пересечении окружностей с прямыми, проведенными через точки \(A\), \(B\) и \(C\), отметим точки \(A_1\), \(B_1\) и \(C_1\). Эти точки будут находиться на тех же прямых, но на расстоянии \(d\) от соответствующих центров.
— Соединим точки \(A_1\), \(B_1\) и \(C_1\) отрезками. Полученная фигура будет треугольником или многоугольником в зависимости от расположения точек.

2) Построение б):

— Построим продолжение прямой \(AC\). Для этого определим уравнение прямой \(AC\) и продлим его в обе стороны.
— Затем построим прямую, проходящую через точку \(B\) и параллельную прямой \(AC\). Уравнение этой прямой будет иметь тот же наклон, что и прямая \(AC\).
— Установим раствор циркуля на длину вектора \(a\) (обозначим его как \(a\)) и проведем дуги с центрами в точках \(A\), \(B\) и \(C\), проходящие через прямые, на которых они лежат.
— Отметим точки \(A_1\), \(B_1\) и \(C_1\) на пересечении дуг и прямых. Эти точки будут находиться на расстоянии \(a\) от центров \(A\), \(B\) и \(C\).
— Соединим точки \(A_1\), \(B_1\) и \(C_1\) отрезками. Полученная фигура также будет многоугольником.

В результате выполнения этих шагов мы получим две фигуры, определенные точками \(A_1\), \(B_1\), \(C_1\) на каждом этапе.