
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1161 Атанасян — Подробные Ответы
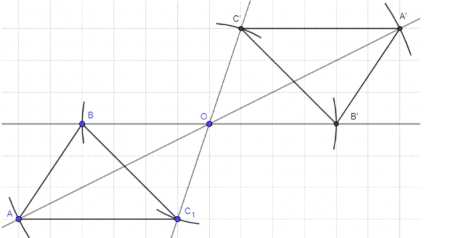
Даны точка О и треугольник ABC. Постройте фигуру F, на которую отображается треугольник ABC при центральной
симметрии с центром О. Что представляет собой фигура F?
Построить: ∆A’B’C’;
Построение:
1) Построим прямые АО, ВО и СО;
3) Построим окружности с центрами в точке О и радиусами ОА, ОВ и ОС;
4) На местах пересечения данных окружностей и прямых отметим точки А’, В’ и С’;
5) Соединим точки А’, В’ и С’;
Ответ: A’B’C’ представляет собой отзеркаленный по двум осям ∆ABC.
Дано: точка О и треугольник ABC.
Требуется построить фигуру F, на которую отображается треугольник ABC при центральной симметрии с центром О.
Решение:
1. Построим прямые АО, ВО и СО, проходящие через вершины треугольника ABC и точку О.
2. Построим окружности с центром в точке О и радиусами ОА, ОВ и ОС.
3. На местах пересечения данных окружностей и прямых отметим точки А’, В’ и С’.
4. Соединим точки А’, В’ и С’ — получим треугольник A’B’C’.
Ответ: Фигура F, на которую отображается треугольник ABC при центральной симметрии с центром О, представляет собой треугольник A’B’C’, являющийся отражением (симметричным изображением) треугольника ABC относительно точки О.
Математически, если координаты вершин треугольника ABC равны (x₁, y₁), (x₂, y₂) и (x₃, y₃), то координаты вершин треугольника A’B’C’ будут равны (-x₁, -y₁), (-x₂, -y₂) и (-x₃, -y₃) соответственно.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!