ГДЗ по Геометрии 9 класс Номер 1160 Атанасян — Подробные Ответы

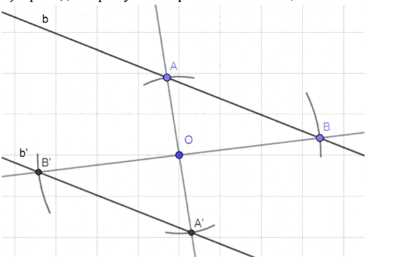
Даны точка О и прямая b. Постройте прямую, на которую отображается прямая b при центральной симметрии с центром О.

Построить: b’;

Построение:
1) Отметим точки А и В на прямой b;
2) Построим прямые АО и ВО;
3) Построим окружности с центрами в точке О и радиусами ОА и ОВ;
4) На местах пересечения данных окружностей и прямых отметим точки А’ и В’;
5) Проведем прямую b’ через точки А’ и В’.

Построить: b’

Построение:
1) Отметим точки А и В на прямой b.
2) Построим прямые АО и ВО.
3) Построим окружности с центрами в точке О и радиусами ОА и ОВ.
4) На местах пересечения данных окружностей и прямых отметим точки А’ и В’.
5) Проведем прямую b’ через точки А’ и В’.

Для построения:

1) Отметим точки А и В на прямой b.
2) Построим прямые АО и ВО.
\(
\text{Уравнение прямой АО: } y = \frac{y_{\text{A}} — y_{\text{O}}}{x_{\text{A}} — x_{\text{O}}}(x — x_{\text{O}}) + y_{\text{O}}
\)
\(
\text{Уравнение прямой ВО: } y = \frac{y_{\text{B}} — y_{\text{O}}}{x_{\text{B}} — x_{\text{O}}}(x — x_{\text{O}}) + y_{\text{O}}
\)
3) Построим окружности с центрами в точке О и радиусами ОА и ОВ.
\(
\text{Уравнение окружности с центром в точке О и радиусом ОА: } (x — x_{\text{O}})^2 +\)
\(+ (y — y_{\text{O}})^2 = \text{ОА}^2
\)
\(
\text{Уравнение окружности с центром в точке О и радиусом ОВ: } (x — x_{\text{O}})^2 +\)
\(+ (y — y_{\text{O}})^2 = \text{ОВ}^2
\)
4) На местах пересечения данных окружностей и прямых отметим точки А’ и В’.
5) Проведем прямую b’ через точки А’ и В’.
\(
\text{Уравнение прямой b’: } y = \frac{y_{\text{B’}} — y_{\text{A’}}}{x_{\text{B’}} — x_{\text{A’}}}(x — x_{\text{A’}}) + y_{\text{A’}}
\)