Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1158 Атанасян — Подробные Ответы
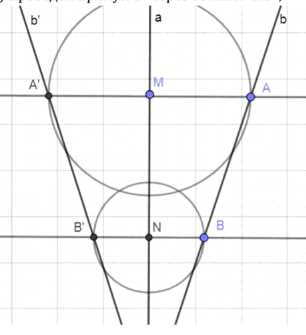
Даны две прямые a и b. Постройте прямую, на которую отображается прямая b при осевой симметрии с осью а.
Построить: b’;
Построение:
1) Отметим точки А и В на прямой b;
2) Проведем перпендикуляры к прямой а через эти точки и отметим точки М и N в местах пересечения перпендикуляров и прямой а;
3) Построим окружности с центрами М и N и радиусами МА и NB;
4) На местах пересечения данных окружностей и перпендикуляров, от отметим точки А’ и В’;
5) Проведем прямую b’ через точки А’ и В’.
Для построения прямой b’, на которую отображается прямая b при осевой симметрии с осью a, выполним следующие действия:
1) Отметим точки А и В на прямой b.
2) Проведем перпендикуляры к прямой a через точки А и В. Отметим точки пересечения этих перпендикуляров с прямой a как M и N соответственно.
3) Построим окружности с центрами в точках M и N и радиусами MA и NB.
4) Найдем точки пересечения построенных окружностей с перпендикулярами к прямой a. Обозначим эти точки как A’ и B’.
5) Проведем прямую b’, проходящую через точки A’ и B’.
Таким образом, прямая b’ является образом прямой b при осевой симметрии относительно прямой a.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.