ГДЗ по Геометрии 9 класс Номер 1157 Атанасян — Подробные Ответы

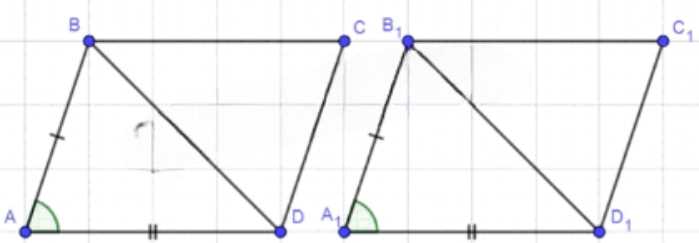
Докажите, что два параллелограмма равны, если смежные стороны и угол между ними одного параллелограмма соответственно равны смежным сторонам и углу между ними другого параллелограмма.

Дано: ABCD, A,B,C,D1- параллелог; AB = A1B1; AD = A1D1; LA = LA1;

Доказательство:
1) Проведем диагонали BD и B1D1;
2) По первому признаку AABD = AA1B1D1, значит существует наложение д: AABD → AA1B1D1, любое наложение является также и движением, то есть д также движение, при котором A → A1, B → B1, D → D1. При этом движении прямая ВС отображается в прямую, параллельную A1D1 и проходящую через точку B1. Такая прямая единственная и это B1C1;
3) Таким образом ВС = B1C1, аналогично DC = D1C1;
4) ВС = B1C1, DC = D1C1, C = BC ∩ DC = B1C1 ∩ D1C1 следовательно С = С1;
5) Получаем, что все четыре вершины ABCD отображаются в соответствующие вершины A1B1C1D1, значит ABCD → A1B1C1D1, это движение также является наложением, значит ABCD = A1B1C1D1, что и требовалось доказать.

Дано: ABCD, A,B,C,D₁- параллелограмм; AB = A₁B₁; AD = A₁D₁; ∠A = ∠A₁;

Доказательство:
1) Проведем диагонали BD и B₁D₁.
2) По первому признаку равенства треугольников, ΔABD = ΔA₁B₁D₁, значит существует наложение δ: ΔABD → ΔA₁B₁D₁. Любое наложение является также и движением, то есть δ также движение, при котором A → A₁, B → B₁, D → D₁. При этом движении прямая ВС отображается в прямую, параллельную A₁D₁ и проходящую через точку B₁. Такая прямая единственная и это B₁C₁.
3) Таким образом, ВС = B₁C₁, аналогично DC = D₁C₁.
4) Так как ВС = B₁C₁, DC = D₁C₁, и C = BC ∩ DC = B₁C₁ ∩ D₁C₁, то следовательно C = C₁.
5) Получаем, что все четыре вершины ABCD отображаются в соответствующие вершины A₁B₁C₁D₁, значит ABCD → A₁B₁C₁D₁, это движение также является наложением, значит ABCD = A₁B₁C₁D₁, что и требовалось доказать.