Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
Почему этот учебник так ценят:
1. Удобная структура.
Все темы разбиты на логичные и последовательные разделы. Это позволяет легко находить нужный материал и шаг за шагом разбираться в геометрии.
2. Понятный язык.
Объяснения написаны так, чтобы даже сложные вещи стали простыми. Автор старается говорить с учениками на доступном и понятном языке.
3. Задачи для всех.
В учебнике есть задания как для новичков, так и для тех, кто хочет углубиться в тему. Это помогает каждому ученику найти что-то по силам и прокачать свои знания.
4. Наглядность.
Рисунки и схемы делают материал более понятным. Они помогают представить фигуры, их свойства и взаимосвязи.
5. Примеры из жизни.
Многие задачи связаны с реальными ситуациями, что делает геометрию ближе к повседневной жизни. Это не просто теория, а то, что можно применить на практике.
6. Помощь для учителей.
Учебник включает советы и рекомендации, которые помогают преподавателям проводить интересные и продуктивные уроки.
Итог:
Учебник Атанасяна — это не просто книга, а настоящий проводник в мир геометрии. Он помогает не только понять предмет, но и полюбить его. С ним учеба становится проще, интереснее и полезнее.
ГДЗ по Геометрии 9 класс Номер 1156 Атанасян — Подробные Ответы
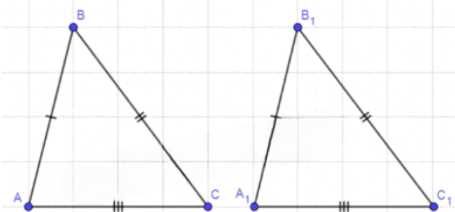
В треугольниках ABC и А1В1С1 AB = А1В1, AC = А1C1, ВС = В1С1. Докажите, что существует движение, при котором точки А, В и С отображаются в точки А1, В1 и С1, и притом только одно.
Решение
По условию задачи треугольники ABC и А1В1С1 равны по трём сторонам. Следовательно, существует наложение, т. е. движение, при котором точки А, В и С отображаются соответственно в точки А1, B1 и С1. Это движение является единственным
движением, при котором точки А, В и С отображаются соответственно в точки A1, В1 и С1 (задача 1155).
Треугольники ABC и A₁B₁C₁ равны по трём сторонам: AB = A₁B₁, AC = A₁C₁, BC = B₁C₁. По признаку равенства треугольников по трём сторонам (SSS) существует движение, которое переводит треугольник ABC в треугольник A₁B₁C₁.
Это движение является единственным, поскольку при равенстве треугольников по трём сторонам положение треугольника в пространстве фиксируется. Таким образом, точки A, B и C отображаются в точки A₁, B₁ и C₁ соответственно, и это наложение может быть выполнено только одним способом.
Рассмотрим треугольники ABC и A₁B₁C₁, для которых по условию задачи выполняются равенства сторон:
1. AB = A₁B₁
2. AC = A₁C₁
3. BC = B₁C₁
Поскольку треугольники равны по трём сторонам (по признаку SSS), мы можем утверждать, что существует такое движение, которое переводит треугольник ABC в треугольник A₁B₁C₁.
Доказательство:
1. По условию равенства сторон, треугольники ABC и A₁B₁C₁ имеют одинаковые размеры и форму.
2. Существует множество движений (повороты, сдвиги, симметрии), которые могут привести один треугольник к другому. Однако, так как мы имеем равенство всех трёх сторон, это накладывает ограничения на возможные движения.
3. Единственное движение, которое может отобразить треугольник ABC в треугольник A₁B₁C₁, будет таким, что:
— точка A переходит в точку A₁,
— точка B переходит в точку B₁,
— точка C переходит в точку C₁.
Таким образом, это движение является единственным, так как любые другие варианты наложения нарушили бы равенство сторон, что противоречит исходному условию.
Следовательно, мы доказали, что существует единственное движение, при котором точки A, B и C отображаются в точки A₁, B₁ и C₁ соответственно.
Геометрия
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.