Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
Почему этот учебник так ценят:
1. Удобная структура.
Все темы разбиты на логичные и последовательные разделы. Это позволяет легко находить нужный материал и шаг за шагом разбираться в геометрии.
2. Понятный язык.
Объяснения написаны так, чтобы даже сложные вещи стали простыми. Автор старается говорить с учениками на доступном и понятном языке.
3. Задачи для всех.
В учебнике есть задания как для новичков, так и для тех, кто хочет углубиться в тему. Это помогает каждому ученику найти что-то по силам и прокачать свои знания.
4. Наглядность.
Рисунки и схемы делают материал более понятным. Они помогают представить фигуры, их свойства и взаимосвязи.
5. Примеры из жизни.
Многие задачи связаны с реальными ситуациями, что делает геометрию ближе к повседневной жизни. Это не просто теория, а то, что можно применить на практике.
6. Помощь для учителей.
Учебник включает советы и рекомендации, которые помогают преподавателям проводить интересные и продуктивные уроки.
Итог:
Учебник Атанасяна — это не просто книга, а настоящий проводник в мир геометрии. Он помогает не только понять предмет, но и полюбить его. С ним учеба становится проще, интереснее и полезнее.
ГДЗ по Геометрии 9 класс Номер 1155 Атанасян — Подробные Ответы
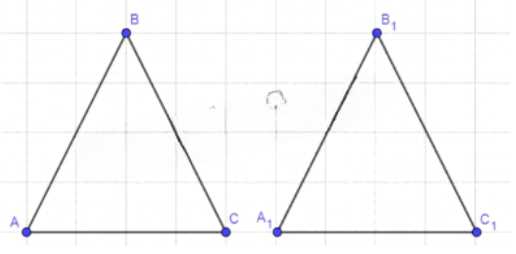
ABC и А1В1С1 — произвольные треугольники. Докажите, что существует не более одного движения, при котором точки
А, В и С отображаются в точки А1, В1, С1.
Пусть A → A1, B → B1, C → C1. Движение сохраняет длину отрезков, значит: A1B1 = AB, B1C1 = BC, A1C1 = AC, следовательно ΔABC = ΔA1B1C1 (по третьему признаку). Существование движения, переводящего данный треугольник в другой, доказано. Пусть точка O — центр окружности, которую можно описать вокруг ΔABC: OA = OB = OC = R. Образ O → O1 также является центром описанной окружности O1A1 = O1B1 = O1C1 = R. Допустим, существует другое движение, отображающее ΔABC → ΔA1B1C1, но вокруг треугольника можно описать только одну окружность, значит эти движения совпадают, то есть 3g — единственное движение.
Дано: ΔABC; ДА, B1 C1;
Доказать: 3g — единственное движение.
Доказательство:
1) Пусть A → A1, B → B1, C → C1.
2) Движение сохраняет длину отрезков, значит: A1B1 = AB, B1C1 = BC, A1C1 = AC, следовательно ΔABC = ΔA1B1C1 (по третьему признаку). Существование движения, переводящего данный треугольник в другой, доказано. При этом полученный треугольник равен исходному.
3) Докажем единственность такого движения. Пусть точка O — центр окружности, которую можно описать вокруг ΔABC: OA = OB = OC = R. Образ O → O1 также является центром описанной окружности O1A1 = O1B1 = O1C1 = R.
4) Допустим, существует другое движение, отображающее ΔABC → ΔA1B1C1, но вокруг треугольника можно описать только одну окружность, значит эти движения совпадают, то есть 3g — единственное движение, что и требовалось доказать.
Геометрия
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.