
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1153 Атанасян — Подробные Ответы
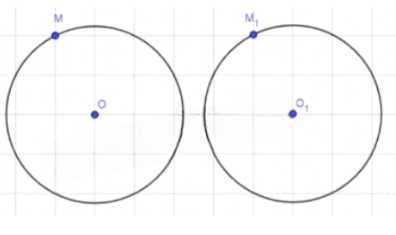
Докажите, что при движении окружность отображается на окружность того же радиуса.
Дано: Окр(O,R); O → O1;
Доказать: R = R1;
Доказательство:
1) Отметим точку M на окружности (O, R), пусть M — M1;
2) Движение сохраняет длину отрезков, значит: OM = R, для любой точки окружности, геометрическое место точек, равноудаленных от O1, это окружность и ее радиус O1M1 = R1 = R, что и требовалось доказать.
Дано: Окр(O,R); O → O₁;
Доказать: R = R₁;
Доказательство:
1) Отметим точку M на окружности (O, R), пусть M — M₁.
2) Движение сохраняет длину отрезков, значит: OM = R, для любой точки окружности, геометрическое место точек, равноудаленных от O₁, это окружность и ее радиус O₁M₁ = R₁.
3) Так как OM = R и O₁M₁ = R₁, то R = R₁, что и требовалось доказать.
Математические формулы:
\(OM = R\)
\(O₁M₁ = R₁\)
\(R = R₁\)
Таким образом, доказано, что радиус окружности Окр(O,R) равен радиусу окружности Окр(O₁,R₁), то есть R = R₁.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!