ГДЗ по Геометрии 9 класс Номер 1152 Атанасян — Подробные Ответы

Докажите, что при движении: а) параллелограмм отображается на параллелограмм; б) трапеция отображается на трапецию; в) ромб отображается на ромб; г) прямоугольник отображается на прямоугольник, а квадрат — на квадрат.

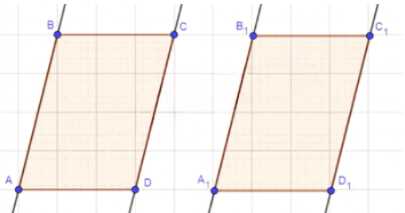
а) Дано: ABCD — параллелограмм; A — A1; B — B1; C — C1; D — D1;
Доказать: A1B1C1D1 — параллелограмм.

Доказательство:
1) ABCD — параллелограмм, следовательно: AB = CD и BC = AD (по свойству параллелограмма).
2) Движение сохраняет длину отрезков, следовательно: A1B1 = AB = CD = C1D1 и B1C1 = BC = AD = A1D1.
Значит A1B1C1D1 — параллелограмм, что и требовалось доказать.

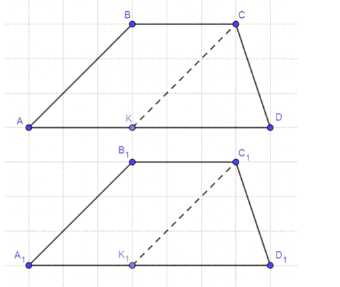
б) Дано: ABCD — трапец; AD || BC; AD > BC; А — А1; В — В1; C — C1; D — D1;
Доказать: A1B1C1D1 — трапеция;

Доказательство:
1) На стороне AD отметим точку К ∈ AD, AK = BC, так как АК || ВС и АК = ВС, то АВСК — параллелограмм;
2) АВСК — параллелограмм, следовательно: АВ = СК и ВС = АК (по свойству параллелограмма);
3) Движение сохраняет длину отрезков, следовательно: A1B1 = AB = CK = C1K1 и B1C1 = BC = AK = A1K1, значит A1B1C1K1 — параллелограмм, отсюда A1 || B1C1 и K1 ∈ A1D1, значит A1D1 || B1C1, следовательно A1B1C1D1 — трапеция, что и требовалось доказать.

в) В данном изображении представлено доказательство того, что фигура ABCD является ромбом. Ключевые моменты:

1) ABCD — ромб, следовательно: AB = BC = CD = AD (по свойству ромба)
2) Движение сохраняет длину отрезков, следовательно: A1B1 = B1C1 = C1D1 = A1D1, значит A1B1C1D1 — ромб, что и требовалось доказать.

г) Дано: ABCD — квадрат; A — A1; B — B1; C — C1; D — D1.
Доказать: A1B1C1D1 — квадрат.

Доказательство:
1) ABCD — квадрат, следовательно: AB = BC = CD = AD; ∠A = ∠B = ∠C = ∠D (по свойству квадрата).
2) Движение сохраняет длину отрезков и углы, следовательно: A1B1 = B1C1 = C1D1 = A1D1 и ∠A = ∠B = ∠C = ∠D, значит A1B1C1D1 — квадрат, что и требовалось доказать.

а) Дано: ABCD — параллелограмм; A — A₁; B — B₁; C — C₁; D — D₁;
Доказать: A₁B₁C₁D₁ — параллелограмм.

Доказательство:
1) ABCD — параллелограмм, следовательно, по свойству параллелограмма \( AB = CD \) и \( BC = AD \).
2) Движение сохраняет длину отрезков, следовательно, \( A₁B₁ = AB = CD = C₁D₁ \) и \( B₁C₁ = BC = AD = A₁D₁ \).
Таким образом, \( A₁B₁C₁D₁ \) — параллелограмм, что и требовалось доказать.

б) Дано: ABCD — трапеция; AD || BC; AD > BC; A — A₁; B — B₁; C — C₁; D — D₁;
Доказать: A₁B₁C₁D₁ — трапеция.

Доказательство:
1) На стороне AD отметим точку K ∈ AD, так что \( AK = BC \). Поскольку \( AK || BC \) и \( AK = BC \), то \( ABKC \) — параллелограмм.
2) Так как \( ABKC \) — параллелограмм, следовательно, \( AB = CK \) и \( BC = AK \) (по свойству параллелограмма).
3) Движение сохраняет длину отрезков, следовательно, \( A₁B₁ = AB = CK = C₁K₁ \) и \( B₁C₁ = BC = AK = A₁K₁ \). Это означает, что \( A₁B₁C₁K₁ \) — параллелограмм.
4) Так как \( A₁B₁C₁K₁ \) — параллелограмм, то \( A₁ || B₁C₁ \) и \( K₁ ∈ A₁D₁ \), следовательно, \( A₁D₁ || B₁C₁ \).
Таким образом, \( A₁B₁C₁D₁ \) — трапеция, что и требовалось доказать.

в) Дано: ABCD — ромб.
Доказательство:
1) ABCD — ромб, следовательно, \( AB = BC = CD = AD \) (по свойству ромба).
2) Движение сохраняет длину отрезков, следовательно, \( A₁B₁ = B₁C₁ = C₁D₁ = A₁D₁ \).
Таким образом, \( A₁B₁C₁D₁ \) — ромб, что и требовалось доказать.

г) Дано: ABCD — квадрат; A — A₁; B — B₁; C — C₁; D — D₁;
Доказать: A₁B₁C₁D₁ — квадрат.

Доказательство:
1) ABCD — квадрат, следовательно, \( AB = BC = CD = AD \) и \( \angle A = \angle B = \angle C = \angle D \) (по свойству квадрата).
2) Движение сохраняет длину отрезков и углы, следовательно, \( A₁B₁ = B₁C₁ = C₁D₁ = A₁D₁ \) и \( \angle A = \angle B = \angle C = \angle D \).
Таким образом, \( A₁B₁C₁D₁ \) — квадрат, что и требовалось доказать.