ГДЗ по Геометрии 9 класс Номер 1149 Атанасян — Подробные Ответы

Докажите, что при центральной симметрии плоскости:
а) прямая, не проходящая через центр симметрии, отображается на параллельную ей прямую;
б) прямая, проходящая через центр симметрии, отображается на себя.

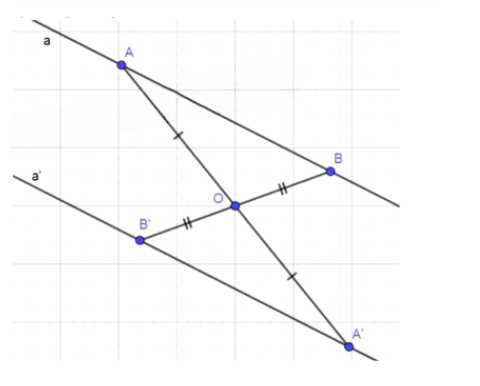
а)

Дано: O — точка симметрии; O-E-a; Доказать: a’ || a;

Доказательство:
1) Отметим случайные точки А и В на прямой а;
2) Так как при симметрии сохраняется расстояние между точками, то АО = A’O и ВО = B’O;
3) Рассмотрим ∆В’ОА’ и ∆ВОА:
∠В’ОА’ = ∠ВОА (как ветрикальные), АО = А’О и ВО = В’О, следовательно ∆В’ОА’ = ∆ВОА (по двум сторонам и углу между ними), ∠В = ∠В’ и ∠А = ∠А’;
4) Рассмотрим прямые АВ и А’B’, BB’ — секущая; ∠В = ∠В’ (как накрестлежащие), значит АВ || AB (по признаку);
5) AB || A’B’ , AB ⊂ a и A’B’ ⊂ a’ значит a || a’ что требовалось доказать.

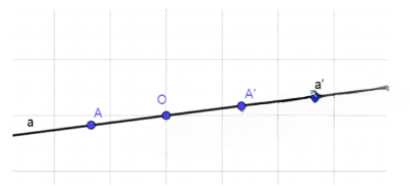
б)

Дано:
0 — точка симметрии;
O Є a;
Доказать: a’ = a;

Доказательство:
1) Отметим случайную точку А на прямой a;
2) АО = A’O, при этом Є a и, так как a’ симметрична a’, то она также проходит через точку O;
3) То есть AO Є a, A’O Є a’, точки А и А’ принадлежат одной прямой;
4) Данное утверждение справедливо для любой точки А, следовательно все точки a Є a’, значит a = a’, что и требовалось доказать.

\(a = a’\)

Доказательство задачи а):

1. Пусть \( O \) — точка симметрии, и \( O \) лежит на прямой \( a \). Обозначим произвольные точки \( A \) и \( B \) на прямой \( a \).

2. По определению симметрии относительно точки \( O \) для точки \( A \) существует точка \( A’ \), такая что \( AO = A’O \) и для точки \( B \) существует точка \( B’ \), такая что \( BO = B’O \).

3. Рассмотрим треугольники \( \Delta B’OA’ \) и \( \Delta BOA \):
— Углы \( \angle B’OA’ \) и \( \angle BOA \) являются вертикальными углами, следовательно, \( \angle B’OA’ = \angle BOA \).
— Так как \( AO = A’O \) и \( BO = B’O \), то по двум сторонам и углу между ними \( \Delta B’OA’ \cong \Delta BOA \).

4. Из равенства треугольников следует, что \( \angle B = \angle B’ \) и \( \angle A = \angle A’ \).

5. Рассмотрим прямые \( AB \) и \( A’B’ \). Поскольку \( B \) и \( B’ \) являются накрест лежащими углами, то \( \angle B = \angle B’ \) означает, что \( AB \parallel A’B’ \) по признаку накрест лежащих углов.

6. Поскольку \( AB \parallel A’B’ \), и \( AB \subset a \), \( A’B’ \subset a’ \), то по свойству параллельных прямых следует, что \( a \parallel a’ \), что и требовалось доказать.

Доказательство задачи б):

1. Пусть \( O \) — точка симметрии, и \( O \in a \). Мы должны доказать, что \( a’ = a \).

2. Обозначим произвольную точку \( A \) на прямой \( a \). По определению симметрии относительно точки \( O \), для точки \( A \) существует точка \( A’ \), такая что \( AO = A’O \).

3. Поскольку \( A \in a \) и \( a’ \) симметрична \( a \), то прямая \( a’ \) также проходит через точку \( O \).

4. Таким образом, точки \( A \) и \( A’ \) принадлежат одной прямой, то есть \( AO \in a \) и \( A’O \in a’ \).

5. Это утверждение верно для любой точки \( A \), следовательно, все точки \( a \in a’ \), что означает, что \( a = a’ \), что и требовалось доказать.

Таким образом, мы получили, что \( a = a’ \).