Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
Почему этот учебник так ценят:
1. Удобная структура.
Все темы разбиты на логичные и последовательные разделы. Это позволяет легко находить нужный материал и шаг за шагом разбираться в геометрии.
2. Понятный язык.
Объяснения написаны так, чтобы даже сложные вещи стали простыми. Автор старается говорить с учениками на доступном и понятном языке.
3. Задачи для всех.
В учебнике есть задания как для новичков, так и для тех, кто хочет углубиться в тему. Это помогает каждому ученику найти что-то по силам и прокачать свои знания.
4. Наглядность.
Рисунки и схемы делают материал более понятным. Они помогают представить фигуры, их свойства и взаимосвязи.
5. Примеры из жизни.
Многие задачи связаны с реальными ситуациями, что делает геометрию ближе к повседневной жизни. Это не просто теория, а то, что можно применить на практике.
6. Помощь для учителей.
Учебник включает советы и рекомендации, которые помогают преподавателям проводить интересные и продуктивные уроки.
Итог:
Учебник Атанасяна — это не просто книга, а настоящий проводник в мир геометрии. Он помогает не только понять предмет, но и полюбить его. С ним учеба становится проще, интереснее и полезнее.
ГДЗ по Геометрии 9 класс Номер 1148 Атанасян — Подробные Ответы
Докажите, что при осевой симметрии плоскости: а) прямая, параллельная оси симметрии, отображается на прямую, параллельную оси симметрии; б) прямая, перпендикулярная к оси симметрии, отображается на себя.
Отобразим условие задачи:
Дано:
l — ось симм;
a ∥ l;
Доказать:
a’ ∥ l;
Доказательство:
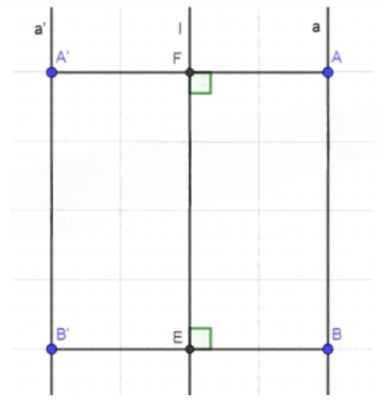
1) Отметим случайные точки А и В на прямой а.
2) Так как при осевой симметрии сохраняется расстояние между точками, то AF = A’F и BE = B’E, при этом АА’ ⊥ и В’B ⊥.
3) АА’ ⊥ BB’ ∥ a ∥ l, следовательно АА’ и ВВ’ ⊥ a, а также АА’ ∥ ВВ’.
4) Отсюда имеем, что в четырехугольнике АА’ВВ’ ∠A = ∠B = 90° и АА’ ∥ ВВ’, АА’ = ВВ’, следовательно АА’ВВ’ — прямоугольник, отсюда А’В’ ⊥ АВ.
5) А’B’ ∈ a’, АВ ∈ a ∥ l, следовательно a’ ∥ l, что и требовалось доказать.
Отобразим условие задачи:
Дано:
l — ось симм;
a ∥ l;
Доказать:
a’ = a;
Доказательство:
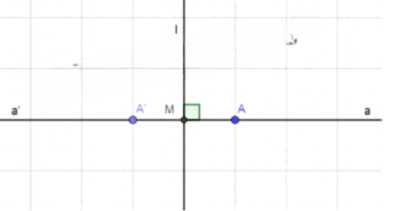
1) Отметим случайную точку А на прямой а.
2) Так как при осевой симметрии сохраняется расстояние между точками, то АМ = A’M, при этом АА’ ⊥.
3) АА’ ⊥ a ∥ l, следовательно либо АА’ ∥ a, либо АА’ ∈ a, но так как А ∈ a, то А’ тоже должна принадлежать a.
4) Данное утверждение справедливо для любой точки А, следовательно все точки a ∈ a’, значит a = a’, что и требовалось доказать.
Отобразим условие задачи:
Дано:
l — ось симм;
a ∥ l;
Доказать:
a’ ∥ l;
Доказательство:
1) Отметим случайные точки А и В на прямой a.
2) Так как при осевой симметрии сохраняется расстояние между точками, то AF = A’F и BE = B’E, при этом АА’ ⊥ и В’B ⊥.
3) АА’ ⊥ BB’ ∥ a ∥ l, следовательно АА’ и ВВ’ ⊥ a, а также АА’ ∥ ВВ’.
4) Отсюда имеем, что в четырехугольнике АА’ВВ’ ∠A = ∠B = 90° и АА’ ∥ ВВ’, АА’ = ВВ’, следовательно АА’ВВ’ — прямоугольник, отсюда А’В’ ⊥ АВ.
5) А’B’ ∈ a’, АВ ∈ a ∥ l, следовательно a’ ∥ l, что и требовалось доказать.
Дано:
l — ось симм;
a ∥ l;
Доказать:
a’ = a;
Доказательство:
1) Отметим случайную точку А на прямой a.
2) Так как при осевой симметрии сохраняется расстояние между точками, то АМ = A’M, при этом АА’ ⊥.
3) АА’ ⊥ a ∥ l, следовательно либо АА’ ∥ a, либо АА’ ∈ a, но так как А ∈ a, то А’ тоже должна принадлежать a.
4) Данное утверждение справедливо для любой точки А, следовательно все точки a ∈ a’, значит a = a’, что и требовалось доказать.
Геометрия
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.