
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1146 Атанасян — Подробные Ответы
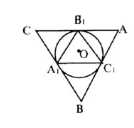
Около данной окружности опишите: а) правильный треугольник; б) правильный шестиугольник.
Согласно изображению, для решения данной задачи необходимо выполнить следующие действия:
1) Отметим случайную точку Н на окружности, построим касательную к окружности через эту точку и восстановим перпендикуляр.
2) Установим циркуль на НО и построим окружность с центром в точке Н, отметим точки пересечения окружностей и повторим данный шаг до тех пор пока не будут отмечены все шесть точек.
3) Точки через одну от Н назовем H1 и Н2 — это высоты и медианы.
a) Отметим точки пересечения безымянных окружностей и прямых, построенных в пункте №1, назовем их А, В и С. Соединим эти точки.
б) Отметим оставшиеся точки Н3, H4, H5 — это середины сторон.
4) Проведем прямые через каждые две противолежащие точки Н.
5) Отметим точки на пересечении этих прямых и окружностей с центром в точках Н, через которые они проходят.
6) Соединим эти точки попарно через одну.
7) Отметим точки А1, А2, А3, А4, A5 и 46 на местах пересечения данных прямых. Соединим эти точки.
Для квадратного уравнения \(ax^2 + bx + c = 0\), решение имеет вид \(x = \frac{-b \pm \sqrt{b^2-4ac}}{2a}\).
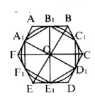
Согласно изображению, для решения данной задачи необходимо выполнить следующие действия:
1) Отметим случайную точку Н на окружности, построим касательную к окружности через эту точку и восстановим перпендикуляр.
2) Установим циркуль на НО и построим окружность с центром в точке Н, отметим точки пересечения окружностей и повторим данный шаг до тех пор, пока не будут отмечены все шесть точек.
3) Точки через одну от Н назовем H₁ и Н₂ — это высоты и медианы.
a) Отметим точки пересечения безымянных окружностей и прямых, построенных в пункте №1, назовем их А, В и С. Соединим эти точки.
б) Отметим оставшиеся точки Н₃, H₄, H₅ — это середины сторон.
4) Проведем прямые через каждые две противолежащие точки Н.
5) Отметим точки на пересечении этих прямых и окружностей с центром в точках Н, через которые они проходят.
6) Соединим эти точки попарно через одну.
7) Отметим точки А₁, А₂, А₃, А₄, A₅ и A₆ на местах пересечения данных прямых. Соединим эти точки.
Для квадратного уравнения \(ax^2 + bx + c = 0\), решение имеет вид \(x = \frac{-b \pm \sqrt{b^2-4ac}}{2a}\).
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!