
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1145 Атанасян — Подробные Ответы
Даны два круга. Постройте круг, площадь которого равна сумме площадей данных кругов.
Построить: окружность с S = S₁ + S₂;
Построение:
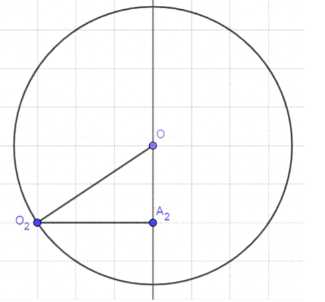
1) Так как S = S₁ + S₂, то R² = R₁² + R₂², следовательно необходимо построить прямоугольный треугольник, где O₁A₁ и O₂A₂ — катеты, тогда гипотенуза будет радиусом окружности;
2) Восстановим перпендикуляр в точке A₂ к отрезку O₂A₂ и отметим точку O на расстоянии A₁O₁;
3) Соединим точки O₂O — это радиус окружности;
4) Построим окружность с центром в точке O через точку O₂.
Построить: окружность с S = S₁ + S₂;
Построение:
1) Так как S = S₁ + S₂, то R² = R₁² + R₂², следовательно необходимо построить прямоугольный треугольник, где O₁A₁ и O₂A₂ — катеты, тогда гипотенуза будет радиусом окружности.
2) Восстановим перпендикуляр в точке A₂ к отрезку O₂A₂ и отметим точку O на расстоянии A₁O₁.
3) Соединим точки O₂O — это радиус окружности.
4) Построим окружность с центром в точке O через точку O₂.
Для построения окружности с площадью S = S₁ + S₂ необходимо:
1) Найти радиус окружности R, используя формулу: \(R^2 = R_1^2 + R_2^2\), где R₁ и R₂ — радиусы окружностей с площадями S₁ и S₂ соответственно.
2) Восстановить перпендикуляр в точке A₂ к отрезку O₂A₂ и отметить точку O на расстоянии A₁O₁.
3) Соединить точки O₂ и O, получив радиус окружности.
4) Построить окружность с центром в точке O и радиусом, равным отрезку O₂O.
Таким образом, мы построили окружность с площадью S = S₁ + S₂, используя данный алгоритм.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!