Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1143 Атанасян — Подробные Ответы
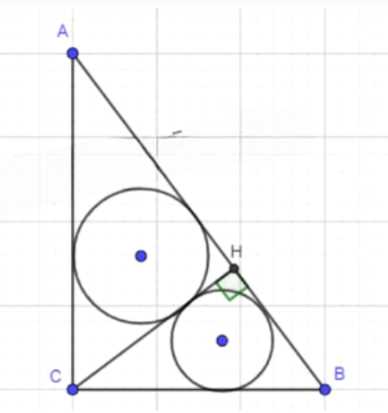
Высота прямоугольного треугольника, проведённая к гипотенузе, разделяет треугольник на два подобных треугольника (см. задачу 2, п. 65). Докажите, что отношение длин окружностей, вписанных в эти треугольники, равно коэффициенту подобия этих треугольников.
Дано: ΔABC — прямоугольный, CH — высота; ΔACH ~ ΔCHB; C₁ — длина окр. вписанной в ΔACH; C₂ — длина окр. вписанной в ΔCHB.
Доказать: C₁ = k; C₂ = k.
Доказательство:
1) Рассмотрим ΔABC — прямоугольный: CH — высота, из того, что ΔACH ~ ΔCHB следует: \(\frac{SACH}{SCHB} = k^2\), где k — коэффициент подобия этих треугольников.
2) \(\frac{S_{ACH}}{S_{CHB}} = \frac{r_1}{r_2}\), где r₁ — радиус вписанной в ΔACH окружности, r₂ — радиус вписанной в ΔCHB окружности.
3) \(\frac{1}{2}r_1 \cdot CH = \frac{1}{2}r_2 \cdot CH\), откуда \(r_1 = r_2\).
4) \(k^2 = \frac{r_1}{r_2} = k \Rightarrow k = 1\).
5) C₁ = 2πr₁, C₂ = 2πr₂, следовательно C₁ = C₂ = k, что и требовалось доказать.
Ответ: C₁ = k, C₂ = k.
Дано: ΔABC — прямоугольный, CH — высота; ΔACH ~ ΔCHB; C₁ — длина окружности, вписанной в ΔACH; C₂ — длина окружности, вписанной в ΔCHB.
Требуется доказать: C₁ = k; C₂ = k.
Доказательство:
1) Рассмотрим ΔABC — прямоугольный треугольник, где CH является высотой. Из того, что ΔACH ~ ΔCHB, следует, что \(\frac{S_{ACH}}{S_{CHB}} = k^2\), где k — коэффициент подобия этих треугольников.
2) Выразим отношение площадей через радиусы вписанных окружностей: \(\frac{S_{ACH}}{S_{CHB}} = \frac{r_1}{r_2}\), где r₁ — радиус окружности, вписанной в ΔACH, r₂ — радиус окружности, вписанной в ΔCHB.
3) Используя формулу для площади треугольника, получаем: \(\frac{1}{2}r_1 \cdot CH = \frac{1}{2}r_2 \cdot CH\), откуда следует, что \(r_1 = r_2\).
4) Подставляя полученное равенство в выражение для коэффициента подобия, имеем: \(k^2 = \frac{r_1}{r_2} = k \Rightarrow k = 1\).
5) Длина окружности вписанной в треугольник равна \(C = 2\pi r\). Следовательно, C₁ = 2πr₁, C₂ = 2πr₂, и, учитывая, что r₁ = r₂, получаем: C₁ = C₂ = k, что и требовалось доказать.
Ответ: C₁ = k, C₂ = k.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.