
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1142 Атанасян — Подробные Ответы
Основания трапеции, около которой можно описать окружность, равны 4 см и 14 см, а одна из боковых сторон равна 13 см. Найдите длину описанной окружности.
Решение:
1) Так как около трапеции можно описать окружность, то она является равнобокой, то есть AB = CD;
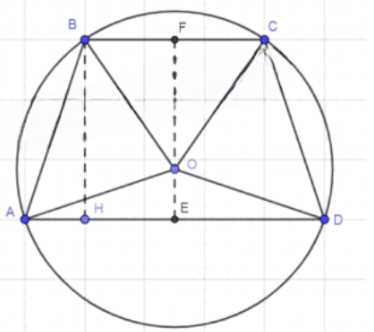
2) Опустим высоту BH, а также FE — серединный перпендикуляр BC и AD, EF = BH = 12 см;
3) Проведем серединный перпендикуляр для стороны BA и отметим точку O на месте его пересечения с FE, O — центр описанной окружности;
4) Рассмотрим ΔABH — прямоугольный:
BH = √(AB² — AH²) = √(169 — 25) = √144 = 12 см
5) OB = OA = R. Пусть OF = x, тогда по теореме Пифагора: R² = x² + BF² = x² + (12 — x)² = x² + 144 — 24x + x² = 2x² — 24x + 144 = 0; 24x = 189 => x = 7,875 см;
R = √(62,015 + 4) = 8,125 см
6) C = 2πR = 16,25π см
Ответ: C = 16,25π см.
Дано: ABCD — трапеция; AB = 13 см; AD = 14 см; BC = 4 см.
Найти: длину дуги C.
Решение:
1) Так как около трапеции можно описать окружность, то она является равнобокой, то есть AB = CD.
2) Опустим высоту BH, а также FE — серединный перпендикуляр BC и AD, EF = BH = 12 см.
3) Проведем серединный перпендикуляр для стороны BA и отметим точку O на месте его пересечения с FE, O — центр описанной окружности.
4) Рассмотрим прямоугольный треугольник ABH:
BH = √(AB² — AH²) = √(169 — 25) = √144 = 12 см.
5) OB = OA = R. Пусть OF = x, тогда по теореме Пифагора: R² = x² + BF² = x² + (12 — x)² = x² + 144 — 24x + x² = 2x² — 24x + 144 = 0;
24x = 189 => x = 7,875 см.
R = √(62,015 + 4) = 8,125 см.
6) Длина дуги C = 2πR = 2π × 8,125 = 16,25π см.
Ответ: длина дуги C = 16,25π см.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!