ГДЗ по Геометрии 9 класс Номер 1138 Атанасян — Подробные Ответы

Найдите длину окружности, вписанной в ромб, если:
а) диагонали ромба равны 6 см и 8 см;
б) сторона ромба равна a и острый угол равен α

Дано:

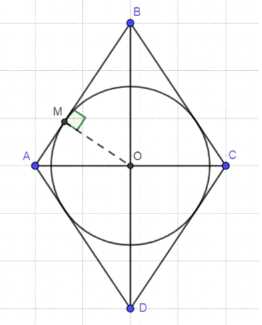
— \( ABCD \) — ромб
— Окружность \((O, r)\) вписана в ромб
— \( AC = 6 \) см
— \( BD = 8 \) см
— \( AB = a \)
— \(\angle ABC = \alpha\)

Найти: \( C \)

Решение:

a)

1) Проведем \( OM \perp AB \) и \( OM = r \).

2) Рассмотрим \(\triangle ABO\) — прямоугольный:

\(
AB = \sqrt{AO^2 + OB^2} = \sqrt{9 + 16} = 5 \text{ см}
\)

(так как \( AO = OC \) и \( BO = OD \) по свойству диагоналей ромба);

3) \( S_{ABO} = \frac{1}{2} \cdot AO \cdot OB = \frac{1}{2} \cdot 4 \cdot 3 = 6 \text{ см}^2 \);

4) \( S_{ABO} = \frac{1}{2} \cdot AB \cdot MO = 6 \text{ см}^2 \Rightarrow OM = \frac{6}{5} = 2,4 \text{ см} \);

5) \( C = 2\pi r = 2 \cdot 3,14 \cdot 2,4 = 15,1 \text{ см} \).

b)

1) \(\angle ABO = \angle OBC = \frac{\alpha}{2}\) (по свойству диагоналей);

2) \(\cos \angle ABO = \frac{OB}{AB} \Rightarrow OB = AB \cdot \cos \angle ABO\);

\(
OB = a \cdot \cos \frac{\alpha}{2}
\)

3) В треугольнике \( \triangle BOM \):

\(
\sin \angle MBO = \frac{OM}{OB} \Rightarrow OM = OB \cdot \sin \angle MBO
\)

\(
OM = a \cdot \cos \frac{\alpha}{2} \cdot \sin \frac{\alpha}{2} = \frac{a}{2} \cdot \sin \alpha
\)

\(
r = \frac{a}{2} \cdot \sin \alpha
\)

4) \( C = 2\pi r = 2\pi \cdot \frac{a}{2} \cdot \sin \alpha = \pi a \cdot \sin \alpha \).

Ответ: a) \( C = 15,1 \) см; b) \( C = \pi a \cdot \sin \alpha \).

Дано:
Ромб \(ABCD\), в который вписана окружность \((O, r)\).
Известно:
Диагонали ромба: \(AC = 6 \, \text{см}\), \(BD = 8 \, \text{см}\).
Сторона ромба: \(AB = a\).
Угол ромба: \(\angle ABC = \alpha\).

Найти:
1) Длину окружности \(C\).

Решение:

1. Определим длину стороны ромба \(AB\).
Диагонали ромба пересекаются под прямым углом и делятся точкой пересечения пополам. Пусть \(O\) — точка пересечения диагоналей. Тогда:
\(
AO = \frac{AC}{2} = \frac{6}{2} = 3 \, \text{см}, \quad BO = \frac{BD}{2} = \frac{8}{2} = 4 \, \text{см}.
\)
В прямоугольном треугольнике \(\triangle ABO\):
\(
AB = \sqrt{AO^2 + BO^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \, \text{см}.
\)

2. Найдем радиус \(r\) вписанной окружности.
Площадь ромба можно выразить через диагонали:
\(
S = \frac{1}{2} \cdot AC \cdot BD = \frac{1}{2} \cdot 6 \cdot 8 = 24 \, \text{см}^2.
\)
Площадь ромба также равна произведению его стороны на высоту:
\(
S = AB \cdot h, \quad h = \frac{S}{AB}.
\)
Подставим значения:
\(
h = \frac{24}{5} = 4 \, \frac{4}{5} \, \text{см} \, \left(\text{или } 4{,}8 \, \text{см}\right).
\)
Высота ромба равна удвоенному радиусу вписанной окружности, то есть:
\(
h = 2r \quad \Rightarrow \quad r = \frac{h}{2} = \frac{4{,}8}{2} = 2{,}4 \, \text{см}.
\)

3. Найдем длину окружности.
Длина окружности выражается формулой:
\(
C = 2\pi r.
\)
Подставим значение радиуса:
\(
C = 2 \cdot 3{,}14 \cdot 2{,}4 = 15{,}072 \, \text{см}.
\)
Округлим до десятых:
\(
C = 15{,}1 \, \text{см}.
\)

4. Выразим длину окружности через параметры \(a\) и \(\alpha\).
Угол \(\angle ABO = \angle OBC = \frac{\alpha}{2}\) (по свойству диагоналей ромба).
В прямоугольном треугольнике \(\triangle ABO\):
\(
\cos \left(\frac{\alpha}{2}\right) = \frac{OB}{AB}, \quad OB = AB \cdot \cos \left(\frac{\alpha}{2}\right) = a \cdot \cos \left(\frac{\alpha}{2}\right).
\)
В треугольнике \(\triangle BOM\):
\(
\sin \left(\frac{\alpha}{2}\right) = \frac{OM}{OB}, \quad OM = OB \cdot \sin \left(\frac{\alpha}{2}\right).
\)
Подставим \(OB\):
\(
OM = a \cdot \cos \left(\frac{\alpha}{2}\right) \cdot \sin \left(\frac{\alpha}{2}\right).
\)
Используем формулу приведения:
\(
\cos \left(\frac{\alpha}{2}\right) \cdot \sin \left(\frac{\alpha}{2}\right) = \frac{1}{2} \sin \alpha.
\)
Тогда:
\(
OM = \frac{a}{2} \cdot \sin \alpha.
\)
Радиус окружности равен \(OM\):
\(
r = \frac{a}{2} \cdot \sin \alpha.
\)
Длина окружности:
\(
C = 2\pi r = 2\pi \cdot \frac{a}{2} \cdot \sin \alpha = \pi a \cdot \sin \alpha.
\)

Ответ:
1) \(C = 15{,}1 \, \text{см}\);
2) \(C = \pi a \cdot \sin \alpha\).