
Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
ГДЗ по Геометрии 9 класс Номер 1137 Атанасян — Подробные Ответы
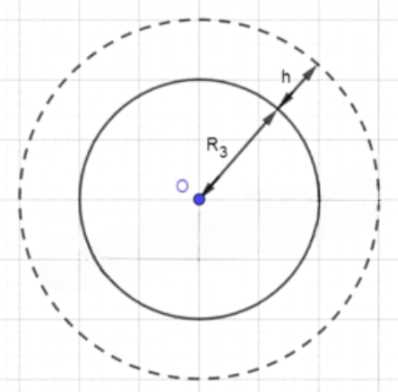
За два оборота по круговой орбите вокруг Земли космический корабль проделал путь 84 152 км. На какой высоте над поверхностью Земли находится корабль, если радиус Земли равен 6370 км?
Дано:
\( n = 2 \) оборота;
\( C_n = 84 \, 152 \) км;
\( R_з = 6 \, 370 \) км;
Найти: \( h \).
Решение:
1) \( C_1 = \frac{84 \, 152}{2} = 42 \, 076 \) км (длина одного оборота);
2) \( C = 2 \pi R \Rightarrow R_{\text{орбиты}} = \frac{S}{2 \pi} = \frac{42 \, 076}{2 \cdot 3,14} = 6 \, 700 \) км;
3) \( R_{\text{орбиты}} = R_з + h \Rightarrow h = R_{\text{орбиты}} — R_з \)
\( h = 6 \, 700 — 6 \, 370 = 330 \) км.
Ответ: космический корабль находится в 330 км над землей.
Дано:
— \( n = 2 \) оборота;
— \( C_n = 84\,152 \) км;
— \( R_з = 6\,370 \) км;
Найти: \( h \).
Решение:
1. Найдем длину одного оборота:
\(
C_1 = \frac{84\,152}{2} = 42\,076 \text{ км}
\)
2. Используем формулу длины окружности, чтобы найти радиус орбиты:
\(
C = 2 \pi R \Rightarrow R_{\text{орбиты}} = \frac{C_1}{2 \pi}
\)
Подставим значения:
\(
R_{\text{орбиты}} = \frac{42\,076}{2 \times 3,14} = \frac{42\,076}{6,28} \approx 6\,700 \text{ км}
\)
3. Найдем высоту \( h \) над Землей:
\(
R_{\text{орбиты}} = R_з + h \Rightarrow h = R_{\text{орбиты}} — R_з
\)
Подставим значения:
\(
h = 6\,700 — 6\,370 = 330 \text{ км}
\)
Ответ: космический корабль находится в 330 км над землей.
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!