ГДЗ по Геометрии 9 класс Номер 1136 Атанасян — Подробные Ответы

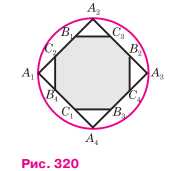
Квадрат А1А2А3А4 вписан в окружность радиуса R (рис. 320). На его сторонах отмечены восемь точек так, что
А1В1 = А2В2 = А3В3 = А4В4 = А1С1 = А2С2 = А3С3 = А4С4 = R. Докажите, что восьмиугольник В1С3В2С4В3С1В4C2 правильный, и выразите площадь этого восьмиугольника через ра диус R.

Дано: \(A_1A_2A_3A_4\) — квадрат, вписанный в окружность радиуса \(R\).

Доказать: \(B_1C_3B_2C_4B_3C_1B_4C_2\) — правильный восьмиугольник.

Выразить: \(S_8\) через \(R\).

Решение:

1. \(A_1B_1 = A_2C_2 = R\); \(A_1A_2 = A_1C_2 + C_2B_1 + B_1A_2\).

Если \(C_2B_1 = x\), то \(x + R — x + R — x = 2R — x = A_1A_2\).

2. \(C_3B_2 = C_4B_3 = C_1B_4 = 2R — A_1A_2\), так как \(A_1A_2 = R\sqrt{2}\), то \(C_2B_1 = \ldots = B_4C_1 = R(2 — \sqrt{2})\).

3. Докажем, что \(C_2B_1 = B_1C_3\):

Рассмотрим \(\triangle A_1B_1C_3\), по теореме Пифагора:

\(
B_1C_3 = \sqrt{2(R — x)^2}
\)

\(
B_1C_3 = \sqrt{2(R — 2R + R\sqrt{2})} = 2R — R\sqrt{2} = R(2 — \sqrt{2})
\)

4. Получаем, что все стороны восьмиугольника равны, значит все его углы также равны, следовательно \(B_1C_3B_2C_4B_3C_1B_4C_2\) — правильный многоугольник, что и требовалось доказать.

5. \(S = 8 \cdot S_{B_1OC_2}\), где \(O\) — точка пересечения диагоналей.

\(
S_{B_1OC_2} = \frac{1}{2} \cdot OB_1 \cdot OC_2 \cdot \sin \angle B_1OC_2
\)

6. \(\angle B_1OC_2 = 45^\circ\) (так как все углы восьмиугольника по \(135^\circ\)).

В \(\triangle AB_1OC_2\): \(\angle B_1 = 67,5^\circ\), \(\angle C_2 = 67,5^\circ\).

7. По теореме косинусов:

\(
(B_1C_2)^2 = (OB_1)^2 + (OC_2)^2 — 2 \cdot OB_1 \cdot OC_2 \cdot \cos 45^\circ
\)

\(
R^2(2-\sqrt{2})^2 = x^2 + x^2 — 2x^2 \cdot \frac{\sqrt{2}}{2}
\)

\(
R^2(2-\sqrt{2})^2 = x^2(2 — \sqrt{2}) \Rightarrow x = R \cdot \sqrt{2 — \sqrt{2}}
\)

8. \(S_{B_1OC_2} = \frac{1}{2} \cdot R \cdot \sqrt{2 — \sqrt{2}} \cdot R \cdot \sqrt{2 — \sqrt{2}} \cdot \sin 45^\circ = \frac{R^2(2 — \sqrt{2})}{2}\).

9. \(S_8 = 8 \cdot \frac{R^2(2 — \sqrt{2})}{2} = 4(R^2(2 — \sqrt{2}))\).

Ответ: \(S_8 = 4(\sqrt{2} — 1)R^2\).

Дано: квадрат \(A_1A_2A_3A_4\) вписан в окружность радиуса \(R\).

Требуется доказать, что восьмиугольник \(B_1C_3B_2C_4B_3C_1B_4C_2\) является правильным и выразить его площадь \(S_8\) через \(R\).

Решение:

1. Найдем длину стороны квадрата. Поскольку квадрат вписан в окружность, его диагональ равна диаметру окружности, то есть \(2R\). Следовательно, сторона квадрата \(A_1A_2 = \frac{2R}{\sqrt{2}} = R\sqrt{2}\).

2. Рассмотрим треугольник \(\triangle A_1B_1C_3\). По теореме Пифагора, можно выразить \(B_1C_3\):

\(
B_1C_3 = \sqrt{(A_1B_1)^2 + (A_1C_3)^2}
\)

Поскольку \(A_1B_1 = A_2C_2 = R\), и \(A_1C_3 = R — x\), где \(x = C_2B_1\).

3. Учитывая, что \(C_2B_1 = x\), можно записать:

\(
A_1A_2 = R\sqrt{2} = R + (R — x) + x
\)

Это упрощается до:

\(
R\sqrt{2} = 2R — x
\)

Таким образом, \(x = 2R — R\sqrt{2}\).

4. Подставим \(x\) в выражение для \(B_1C_3\):

\(
B_1C_3 = \sqrt{R^2 + (R — (2R — R\sqrt{2}))^2}
\)

\(
B_1C_3 = \sqrt{R^2 + (R\sqrt{2} — R)^2}
\)

\(
B_1C_3 = \sqrt{R^2 + (R(\sqrt{2} — 1))^2}
\)

\(
B_1C_3 = R(\sqrt{2} — 1)
\)

5. Таким образом, все стороны восьмиугольника равны \(B_1C_3 = C_2B_1 = R(\sqrt{2} — 1)\), что делает его правильным восьмиугольником.

6. Теперь найдем площадь восьмиугольника. Площадь правильного восьмиугольника можно найти как сумму площадей восьми равнобедренных треугольников с вершинами в центре окружности.

7. Площадь одного такого треугольника \(S_{\triangle} = \frac{1}{2} \cdot OB_1 \cdot OC_2 \cdot \sin(45^\circ)\), где \(OB_1 = OC_2 = R\).

\(
S_{\triangle} = \frac{1}{2} \cdot R \cdot R \cdot \frac{\sqrt{2}}{2} = \frac{R^2\sqrt{2}}{4}
\)

8. Площадь восьмиугольника \(S_8 = 8 \cdot S_{\triangle} = 8 \cdot \frac{R^2\sqrt{2}}{4} = 2R^2\sqrt{2}\).

9. Преобразуем полученное выражение в удобную форму:

\(
S_8 = 4(\sqrt{2} — 1)R^2
\)

Таким образом, мы доказали, что восьмиугольник является правильным, и выразили его площадь через радиус окружности. Ответ: \(S_8 = 4(\sqrt{2} — 1)R^2\).