ГДЗ по Геометрии 9 класс Номер 1133 Атанасян — Подробные Ответы

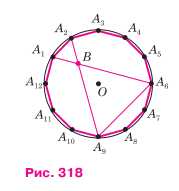
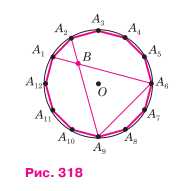
Диагонали А1А6 и A2A9 правильного двенадцатиугольника пересекаются в точке B (рис. 318). Докажите, что: а) треугольники A1A2B и A6A9B равносторонние; б) А1А6 = 2r, где r — радиус вписанной в двенадцатиугольник окружности.

Дано: \(A_1A_2 \ldots A_{12}\) — правильный 12-угольник; \(A_1A_6 \cap A_2A_9 = B\).

Доказать:
а) \(\triangle A_1A_2B\) и \(\triangle A_6A_9B\) — правильные;
б) \(A_1A_6 = 2r\).

Доказательство:

а) Так как правильный многоугольник вписан в окружность, то каждая дуга равна:
\( A_1A_2 = A_2A_3 = \ldots = A_{11}A_{12} = \frac{360^\circ}{12} = 30^\circ \)

\(
\angle A_2A_1B = \frac{1}{2} \angle A_2A_4A_6 = \frac{1}{2} \cdot 120^\circ = 60^\circ
\)

\(
\angle A_1A_2B = \frac{1}{2} \angle A_1A_{11}A_9 = \frac{1}{2} \cdot 120^\circ = 60^\circ
\)

\(
\angle A_9A_6B = \frac{1}{2} \angle A_2A_4A_6 = \frac{1}{2} \cdot 120^\circ = 60^\circ
\)

\(
\angle A_6A_9B = \frac{1}{2} \angle A_1A_{11}A_9 = \frac{1}{2} \cdot 120^\circ = 60^\circ
\)

Так как сумма углов в треугольнике 180°:
\(\angle A_1BA_2 = \angle A_6BA_9 = 60^\circ\), следовательно, \(\triangle A_1A_2B\) и \(\triangle A_6A_9B\) — правильные, что и требовалось доказать.

б) \(\angle A_1A_6A_9\) — вписанный, \(\angle A_1A_6A_9 = \frac{1}{2} \angle A_1A_{10}A_7 = 90^\circ\), следовательно, \(A_6A_1 \perp A_1A_{12}\) и \(OH_2 \perp A_1A_{12}\); \(OH_2 \parallel A_1A_6\).

Так же и \(\angle A_1A_{12}A_6 = 90^\circ\), \(A_1A_6 \perp A_6A_9\) и \(OH_1 \perp A_6A_9\); \(OH_1 \parallel A_1A_6\).

Получаем, что \(A_1A_6H_1H_2\) — прямоугольник, отсюда \(A_1A_6 = H_1H_2 = 2r\), что и требовалось доказать.

Дано: \(A_1A_2 \ldots A_{12}\) — правильный 12-угольник; \(A_1A_6 \cap A_2A_9 = B\).

Доказать:
а) \(\triangle A_1A_2B\) и \(\triangle A_6A_9B\) — правильные;
б) \(A_1A_6 = 2r\).

Решение:

а) Так как правильный многоугольник вписан в окружность, то каждая дуга равна:
\( A_1A_2 = A_2A_3 = \ldots = A_{11}A_{12} = \frac{360^\circ}{12} = 30^\circ \)

Углы при вершинах треугольников можно найти как половину соответствующих центральных углов:

\(
\angle A_2A_1B = \frac{1}{2} \times 120^\circ = 60^\circ
\)

\(
\angle A_1A_2B = \frac{1}{2} \times 120^\circ = 60^\circ
\)

\(
\angle A_9A_6B = \frac{1}{2} \times 120^\circ = 60^\circ
\)

\(
\angle A_6A_9B = \frac{1}{2} \times 120^\circ = 60^\circ
\)

Так как сумма углов в треугольнике равна 180°, то:

\(
\angle A_1BA_2 = 180^\circ — (\angle A_2A_1B + \angle A_1A_2B) = 180^\circ — 120^\circ = 60^\circ
\)

\(
\angle A_6BA_9 = 180^\circ — (\angle A_9A_6B + \angle A_6A_9B) = 180^\circ — 120^\circ = 60^\circ
\)

Следовательно, \(\triangle A_1A_2B\) и \(\triangle A_6A_9B\) — правильные треугольники, так как все углы равны \(60^\circ\), что и требовалось доказать.

б) Угол \(\angle A_1A_6A_9\) — вписанный, он равен половине центрального угла \(\angle A_1A_{10}A_7\), который равен \(180^\circ\), следовательно:

\(
\angle A_1A_6A_9 = \frac{1}{2} \times 180^\circ = 90^\circ
\)

Таким образом, \(A_1A_6\) является диаметром окружности, описанной около прямоугольного треугольника \(A_1A_6A_9\). Поскольку радиус окружности равен \(r\), то диаметр равен \(2r\).

Следовательно, \(A_1A_6 = 2r\), что и требовалось доказать.