Учебник по геометрии для 7-9 классов, написанный Атанасяном, — это настоящий помощник для школьников и учителей. Он не только помогает разобраться в сложных темах, но и делает процесс изучения интересным и понятным.
Почему этот учебник так ценят:
1. Удобная структура.
Все темы разбиты на логичные и последовательные разделы. Это позволяет легко находить нужный материал и шаг за шагом разбираться в геометрии.
2. Понятный язык.
Объяснения написаны так, чтобы даже сложные вещи стали простыми. Автор старается говорить с учениками на доступном и понятном языке.
3. Задачи для всех.
В учебнике есть задания как для новичков, так и для тех, кто хочет углубиться в тему. Это помогает каждому ученику найти что-то по силам и прокачать свои знания.
4. Наглядность.
Рисунки и схемы делают материал более понятным. Они помогают представить фигуры, их свойства и взаимосвязи.
5. Примеры из жизни.
Многие задачи связаны с реальными ситуациями, что делает геометрию ближе к повседневной жизни. Это не просто теория, а то, что можно применить на практике.
6. Помощь для учителей.
Учебник включает советы и рекомендации, которые помогают преподавателям проводить интересные и продуктивные уроки.
Итог:
Учебник Атанасяна — это не просто книга, а настоящий проводник в мир геометрии. Он помогает не только понять предмет, но и полюбить его. С ним учеба становится проще, интереснее и полезнее.
ГДЗ по Геометрии 9 класс Номер 1131 Атанасян — Подробные Ответы
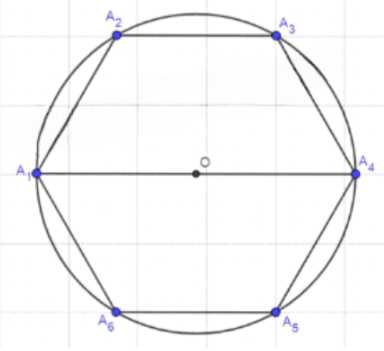
Найдите периметр правильного шестиугольника А1А2А3А4А5А6, если A1A4 = 2,24 см.
Дано: правильный шестиугольник \(A_1A_2A_3A_4A_5A_6\), \(A_1A_4 = 2,24 \, \text{см}\).
Найти: периметр \(P\).
Решение:
1. Диагональ \(A_1A_4\) равна удвоенному радиусу описанной окружности:
\(
2R = 2,24 \, \text{см}
\)
\(
R = \frac{2,24}{2} = 1,12 \, \text{см}
\)
2. Сторона шестиугольника \(a_6\) находится по формуле:
\(
a_6 = 2R \cdot \sin\left(\frac{180^\circ}{6}\right)
\)
\(
a_6 = 2 \cdot 1,12 \cdot \sin 30^\circ = 2 \cdot 1,12 \cdot 0,5 = 1,12 \, \text{см}
\)
3. Периметр шестиугольника:
\(
P = 6 \cdot a_6 = 6 \cdot 1,12 = 6,72 \, \text{см}
\)
Ответ: \(P = 6,72 \, \text{см}\).
Дано: правильный шестиугольник \(A_1A_2A_3A_4A_5A_6\), диагональ \(A_1A_4 = 2,24 \, \text{см}\).
Необходимо найти периметр шестиугольника \(P\).
Решение:
1. Для правильного шестиугольника диагональ \(A_1A_4\) равна удвоенному радиусу описанной окружности. Это связано с тем, что диагональ проходит через центр окружности и соединяет противоположные вершины. Таким образом, имеем:
\(
2R = 2,24 \, \text{см}
\)
Отсюда радиус окружности:
\(
R = \frac{2,24}{2} = 1,12 \, \text{см}
\)
2. Сторона правильного шестиугольника \(a_6\) может быть найдена через радиус описанной окружности. Формула для стороны правильного шестиугольника через радиус описанной окружности:
\(
a_6 = 2R \cdot \sin\left(\frac{180^\circ}{6}\right)
\)
Подставим известные значения:
\(
a_6 = 2 \cdot 1,12 \cdot \sin 30^\circ = 2 \cdot 1,12 \cdot 0,5
\)
\(
a_6 = 2 \cdot 1,12 \cdot 0,5 = 1,12 \, \text{см}
\)
3. Периметр правильного шестиугольника равен сумме длин всех его сторон. Поскольку шестиугольник правильный, все его стороны равны. Таким образом, периметр \(P\) равен:
\(
P = 6 \cdot a_6 = 6 \cdot 1,12
\)
\(
P = 6,72 \, \text{см}
\)
Ответ: периметр шестиугольника \(P = 6,72 \, \text{см}\)
Геометрия
Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.