ГДЗ по Геометрии 9 класс Номер 1124 Атанасян — Подробные Ответы

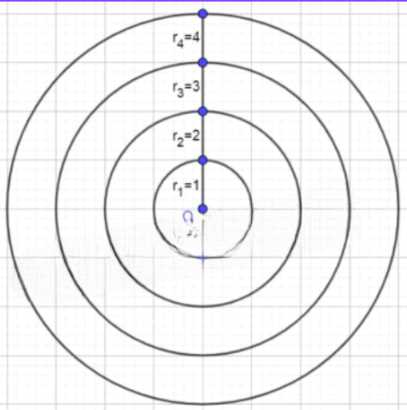
На мишени имеются четыре окружности с общим центром, радиусы которых равны 1, 2, 3 и 4. Найдите площадь наименьшего круга, а также площадь каждого из трёх колец мишени.

Дано: \( r_1 = 1 \), \( r_2 = 2 \), \( r_3 = 3 \), \( r_4 = 4 \).

Найти: \( S_1 \), \( S_{2к} \), \( S_{3к} \), \( S_{4к} \).

Решение:

1. \( S_1 = \pi \cdot (r_1)^2 = \pi \cdot 1^2 = \pi \).

2. \( S_2 = \pi \cdot (r_2)^2 = \pi \cdot 2^2 = 4\pi \).

3. \( S_3 = \pi \cdot (r_3)^2 = \pi \cdot 3^2 = 9\pi \).

4. \( S_4 = \pi \cdot (r_4)^2 = \pi \cdot 4^2 = 16\pi \).

5. \( S_{2к} = S_2 — S_1 = 4\pi — \pi = 3\pi \).

6. \( S_{3к} = S_3 — S_2 = 9\pi — 4\pi = 5\pi \).

7. \( S_{4к} = S_4 — S_3 = 16\pi — 9\pi = 7\pi \).

Ответ: \( S_1 = \pi \); \( S_{2к} = 3\pi \); \( S_{3к} = 5\pi \); \( S_{4к} = 7\pi \).

Дано: радиусы окружностей \( r_1 = 1 \), \( r_2 = 2 \), \( r_3 = 3 \), \( r_4 = 4 \).

Необходимо найти площади \( S_1 \), \( S_{2к} \), \( S_{3к} \), \( S_{4к} \).

Решение:

1. Вычислим площадь круга с радиусом \( r_1 \):
\(
S_1 = \pi \cdot (r_1)^2 = \pi \cdot 1^2 = \pi
\)

2. Вычислим площадь круга с радиусом \( r_2 \):
\(
S_2 = \pi \cdot (r_2)^2 = \pi \cdot 2^2 = 4\pi
\)

3. Вычислим площадь круга с радиусом \( r_3 \):
\(
S_3 = \pi \cdot (r_3)^2 = \pi \cdot 3^2 = 9\pi
\)

4. Вычислим площадь круга с радиусом \( r_4 \):
\(
S_4 = \pi \cdot (r_4)^2 = \pi \cdot 4^2 = 16\pi
\)

5. Найдем площадь кольца между кругами с радиусами \( r_2 \) и \( r_1 \):
\(
S_{2к} = S_2 — S_1 = 4\pi — \pi = 3\pi
\)

6. Найдем площадь кольца между кругами с радиусами \( r_3 \) и \( r_2 \):
\(
S_{3к} = S_3 — S_2 = 9\pi — 4\pi = 5\pi
\)

7. Найдем площадь кольца между кругами с радиусами \( r_4 \) и \( r_3 \):
\(
S_{4к} = S_4 — S_3 = 16\pi — 9\pi = 7\pi
\)

Ответы:

— Площадь первого круга: \( S_1 = \pi \)
— Площадь кольца между кругами с радиусами \( r_2 \) и \( r_1 \): \( S_{2к} = 3\pi \)
— Площадь кольца между кругами с радиусами \( r_3 \) и \( r_2 \): \( S_{3к} = 5\pi \)
— Площадь кольца между кругами с радиусами \( r_4 \) и \( r_3 \): \( S_{4к} = 7\pi \)